Szybkie łamigłówki andrzej: Gdyby ktoś się nudził: 1)Wykazać, że sin(x+y)=sinxcosy+cosxsiny, oraz, że cos(x+y)=cosxcosy−sinxsiny 2)Układając i rozwiązując odpowiednie równanie różniczkowe udowodnić "jedynkę trygonometryczną"

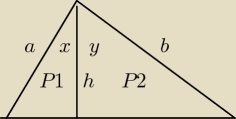
AS: P = P1 + P2

1		1		1		1
	a*b*sin(x + y) =		a*h*sin(x) +		*h*b*sin(y) | :		*a*b
2		2		2		2

	h		h
sin(x + y) =		*sin(x) +		*sin(y)
	b		a

	h		h
ale		= cos(y) ,		= cos(x)
	b		a

stąd związek sin(x + y) = sin(x)*cos(y) + cos(x)*sin(y) cos(x + y) = sin[90 − (x + y)] = sin[(90 − x) + (−y)] na podstawie poprzedniego związku mamy cos(x + y) = sin(90 − x)*cos(−y) + cos(90 − x)*sin(−y) cos(x + y) = cos(x)*cos(y) − sin(x)*sin(y)

andrzej: ja 1−sze zrobiłem następującą metodą: e^ix=cosx+isinx, zatem e^iy=cosy+isiny,zatem e^ix+iy=cos(x+y)+isin(x+y)=e^ix*e^iy, zatem (cosx+isinx)(cosy+isiny)=cos(x+y)+isin(x+y) wszystko wymnażamy, część rzeczywista prawej równa się rzeczywistej lewej, podobnie z częścią urojoną i otrzymujemy powyższe tożsamości.

b.: w takim zadaniu trzeba by określić, jaka jest definicja funkcji cos i sin

Radosław 2: W zadaniu drugim powinno wyjśc.że np rozwiązaniem równania ( y')²+y²=1 jest sinx

Jack: faktycznie jest, wystarczy podstawić i sprawdzić. Ale czy o takie równanie różniczkowe chodzi?

Jack: tfu, nie można podstawiać bo nie ma czego sprawdzać Rozwiązania mają taką postać: y(x)=1−2sin²(¹₂(±t−ic₁) )

Jack: y'²+y²=1 y'=√1−y²

dy
	=√1−y2
dx

dy
	=dx y≠±1
±√1−y2

	dy		dy
1.		=dx 2.		=dx
	+√1−y2		−√1−y2

	dy		dy
∫		=∫dx ∫		=∫dx
	+√1−y2		−√1−y2

arcsiny=x+c dla y<1 arccosy=x+c dla y<1 y=sin(x+c) y=cos(x+c) dla y=±1 również mamy rozwiązanie. Jak zapisał Radosław 2 otrzymujemy w ten sposób dowód jedynki tryg.

b.:

	1
a skad wiemy, ze (arcsiny)' =		? a no m.in. stad, ze znamy jedynke trygonometryczna
	1−y2

dlatego ten powyzszy rachunek nie dowodzi wiec wcale jedynki... w takiej sytuacji trzeba dobrze okreslic, co oznacza sin i cos, i wywnioskowac ,,jedynke'' z przyjetej definicji.

Jack: no wlasnie, zastanawiałem się nad tym, ale nie widziałem w dowodzie w tym kroku wykorzystanej jedynki. Mógłbyś dać link do czytelnego dowodu?

b.: jesli y=sin x, gdzie x∊(−π/2, π/2), to z tw. o pochodnej funkcji odwrotnej mamy

	1		1
(arcsin)' (y) =		=		=...
	(sin)'(x)		cos x

i teraz z jedynki (i tego, ze w naszej sytuacji cosx>0)

	1
... =
	√1−y2

Jack: ok, teraz widzę...

Basia: A kto pamięta dowód dla kąta uogólnionego bez użycia liczb zespolonych ? Dowód Asa jest poprawny tylko dla x,y spełniających warunki: 1. x,y∊(0;π) 2. x+y∊(0;π)

b.: to chyba mozna dostac juz z rozwiazania Asa, stopniowo uogolniajac, np. gdy x,y∊(0;π) , ale x+y≥π, to x≥π/2 lub y ≥π/2, zalozmy np. ze x≥π/2, wtedy sin(x+y) = sin((x−π/2) + y + π/2) = cos((x−π/2) + y) =... (z juz udowodnionego wzoru) ...= cos(x−π/2)cos y − sin(x−π/2)siny = sinx cosy + cosx siny itd., dosc to meczaca metoda, ale mysle, ze da rade

Basia: ten dowód z całą pewnością znałam w III licealnej i nie był jakiś strasznie skomplikowany, ale nijak sobie nie potrafię przypomnieć a może rzeczywiście to było uogólnienie dowodu Asa w oparciu o kąt 2π−(x+y) gdy x+y>π to sobie chyba potrafię wyobrazić no a przypadki x+y=0 x+y=π też łatwo udowodnić