Prosze
Kamil: Pomóżcie prosze,1.Kolejne wyrazy ciągu(a
n) wyznacza się, stosując pewną regułę.
Odkryj tę regułę i zachowując ją, określ wzorem n−ty wyraz ciągu(a
n) o początkowych wyrazach:
| | 1 | | 1 | | 1 | | 1 | |
a)1, |
| , |
| , |
| , |
| ,.....,
|
| | 3 | | 5 | | 7 | | 9 | |
| | 1 | | 1 | | 1 | | 1 | |
b)1, |
| , |
| , |
| , |
| ,.....,
|
| | 4 | | 9 | | 16 | | 25 | |
c)4,7,10,13,16,...,
d)1,
√2,
√3,2,
√5,....,
2.Narysuj wykres ciągu (a
n) określonego wzorem:
| | n−1 | |
b)an= |
| i nε{1,2,3,4}
|
| | n+1 | |
c)a
n=n
2−4,gdy 1≤n<4
d)a
n=(−1)
n−1 i nε{1,2,3,4,5,6}
21 lip 12:29
b.: musisz odkryc te reguly, to naprawde nietrudne, opisz je slowami
(np. w a i b popatrz na mianowniki kolejnych ulamkow)
21 lip 14:35
Godzio:
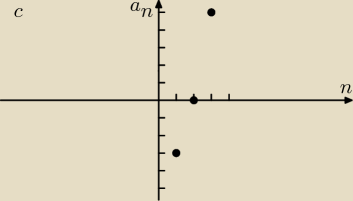
a)
d)
a
n =
√n
musisz kombinować
wykres to poprostu punkty podstawiaj n pod wzór i zaznaczaj te punkty na wykresie
c)
21 lip 15:55
Godzio: Nie da się wytłumaczyć pierwszego musisz tak wykombinować żebyś otrzymać ten ciąg
popatrz na c) powiedz mi co trzeba zrobić żeby pierwszym wyrazem ciągu była liczba 4 ?
21 lip 16:00
Kamil: mówisz o pierwszym zadaniu podpunkt a) tak
21 lip 16:02
Godzio: teraz o c)
21 lip 16:03
Godzio:
masz taki ciąg :
4,7,10,13,16...
Co musisz zrobić żeby ta 4 była pierwszym wyrazem ciągu
21 lip 16:03
Godzio: Podpowiem musisz + 4
Teraz powiedz o ile różnią się kolejne wyrazy ciągu ?
21 lip 16:09
Kamil: o 3
21 lip 16:13
Kamil: i co dalej robić
21 lip 16:14
Godzio: dobrze
czyli do tej 4 trzeba dodawać 3
czyli np. żeby otrzymać 13 trzeba dodać 3*3 i wtedy mamy
4 + 3 * 3 = 13
teraz pomysl jak zapisać to ogólnym wzorem
3 *.... + 4 ?
21 lip 16:15
Kamil: kolejne wyrazy różnią się o 3
21 lip 16:16
Godzio: Czy taki zapis jest poprawny ? :
3n + 4 ?
21 lip 16:18
Kamil: wstawić na n−ty wyraz ciągu
21 lip 16:18
Kamil: no
21 lip 16:18
Godzio:
no właśnie nie bo musisz pamiętać że n ∊ N+ więc n ≠ 0
więc co trzeba jeszcze tam dopisać żeby
3 *(n − ... ) + 4
co trzeba wstawić za " ... " żeby pierwszy wyraz równał się zero ?
21 lip 16:20
Kamil: poprawny jest tak
21 lip 16:20
Kamil: 0
21 lip 16:23
Kamil: 3
21 lip 16:25
Kamil: jestes
21 lip 16:26
Godzio:
pierwszy wyraz jest dla n = 1 ... ehhh Kamil Kamil
więc żeby n − ... = 0 to ... = 1
Odpowiedź
a
n = 3(n − 1) + 4
teraz b) zapisz Ci prostszą postać a ty pomyśl
SAM
| | 1 | | 1 | | 1 | | 1 | |
1, |
| , |
| , |
| , |
| .... |
| | 4 | | 9 | | 16 | | 25 | |
| | 1 | | 1 | | 1 | | 1 | | 1 | |
( |
| )2, ( |
| )2, ( |
| )2,( |
| )2,( |
| )2... |
| | 1 | | 2 | | 3 | | 4 | | 5 | |
postaraj się
21 lip 16:26
Kamil: w ksiązce odpowiedz do a) jest inna
21 lip 16:27
Kamil: | | 1 | |
an= |
| tak jest odpowiedz do a) |
| | 2n−1 | |
21 lip 16:29
Kamil: jestes
21 lip 16:29
Godzio: a no tak tak, źle popatrzyłem na ten ciąg
w takim razie bedziesz mial okazje sam dojsc

| | 1 | | 1 | | 1 | | 1 | |
a) 1, |
| , |
| , |
| , |
| ... |
| | 3 | | 5 | | 7 | | 9 | |
widać że mianowniki ułamków są liczbami nieparzystymi.
ogólnie liczbę nieparzystą można zapisać: 2n − 1 dla n ∊ N
+ kombinuj

powodzenia w a i b
nic więcej juz nie powiem
21 lip 16:30
Kamil: nie wiem skad sie wzieło w tym podpunkcie a) taki wynik an={1}{2n−1}
21 lip 16:45
Kamil: | | 1 | |
nie rozumiem skąd wzioł się taki wynik an= |
| |
| | 2n−1 | |
21 lip 16:48
Kamil: 1,3,5,7,9 te kolejne wyrazt różnią się o 2
21 lip 17:05
Kamil: Co musze zrobić zeby ta 1 była piewszym wyrazem ciągu
21 lip 17:10
Kamil: −1
21 lip 17:11
Kamil: trzeba +1
21 lip 17:15
Kamil: 1+2=3
21 lip 17:22
Kamil: nie rozumiem do końca zadania powiesz co dalej robić
21 lip 17:28
21 lip 17:29
b.: 1,3,5,7,9 te NIE są kolejne wyrazy, tylko MIANOWNIKI kolejnych wyrazów
mianowniki mają więc postać 2n−1
stąd postać na an
21 lip 20:16
 a)
a)

 powodzenia w a i b
nic więcej juz nie powiem
powodzenia w a i b
nic więcej juz nie powiem


