trygonometria
domcia: tgα=√3, α∊(0,90), oblicz sinα + cosα
20 lip 21:12
think: można to zrobić na wiele sposobów, np:
| | sinα | |
tgα = √3 ⇒ |
| = √3 ⇒ sinα = √3cosα |
| | cosα | |
sin
2α + cos
2α = 1
(
√3cosα)
2 + cos
2α = 1
4cos
2α = 1
| | 1 | | 1 | |
cos2α = |
| ⇒ cosα = |
| (odrzucamy rozwiązanie ujemne, bo sin, cos, tg i ctg są |
| | 4 | | 2 | |
dodatnie w podanym przedziale α)
| | 1 | | √3 | |
sinα = √3cosα = √3* |
| = |
| |
| | 2 | | 2 | |
| | 1 | |
sinα + cosα = |
| (1 + √3) |
| | 2 | |
20 lip 21:22
Franek:

proponuję tak: (bo najprościej)
tgα=
√3 =>
α= 60o
cos60
o=
12
| | 1 | | 1 | | 1 | |
sinα+cosα= |
| √3+ |
| = |
| ( √3+1) |
| | 2 | | 2 | | 2 | |
20 lip 22:41
Godzio:
To był nokaut

20 lip 22:48
Franek:


20 lip 22:49
Godzio: szczerze to za szybko bym nie wpadł na ten sposób

20 lip 22:50
Franek:
Eeee
tam ..... nie wierzę

20 lip 22:52
think: wiem Eto

20 lip 22:55
think: Godzio polecam ból głowy gigant, od razu będziesz wpadał na różne pomysły, raju co za ulga,
właśnie mi przechodzi

20 lip 22:57
Godzio: wypróbuje

20 lip 22:58
b.: rozwiązanie ,,think'' jest całkiem ładne: działa też dla innych niż √3 wartości tangensa
20 lip 23:34
think: dziękuję Ci b.

od razu mi lepiej

tym bardziej, że przez jedną krótką chwilę chciałam to
zrobić tak jak Eta, ale zachciało mi się odmiany

20 lip 23:52
Franek:

dla
Lucynki 
20 lip 23:54
think: mówił Ci ktoś Eto, że jesteś

21 lip 00:01
Franek:
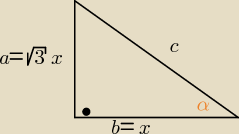
No to jeszcze jeden sposób ( tylko
dla kątów ostrych )
tgα=
√3
tgα=
ab =
√3*xx . x>0
c
2= a
2+b
2 => c
2= 3x
2+x
2= 4x
2
c= 2x

21 lip 00:05
Franek:
Mówił, mówił

moja "połowica" dzień w dzień przez ponad 35 lat


21 lip 00:07
think: dobrze mieć takiego prawdomównego połowca

21 lip 00:10
Franek:
Hehe ....... "szukajcie, a znajdziecie"

21 lip 00:11
think: szukam... ale przeważnie boję się tego co udaje mi się znaleźć.
21 lip 00:14
 proponuję tak: (bo najprościej)
tgα= √3 => α= 60o
proponuję tak: (bo najprościej)
tgα= √3 => α= 60o








 od razu mi lepiej
od razu mi lepiej  tym bardziej, że przez jedną krótką chwilę chciałam to
zrobić tak jak Eta, ale zachciało mi się odmiany
tym bardziej, że przez jedną krótką chwilę chciałam to
zrobić tak jak Eta, ale zachciało mi się odmiany
 dla Lucynki
dla Lucynki 

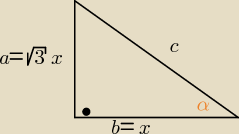 No to jeszcze jeden sposób ( tylko dla kątów ostrych )
tgα= √3
tgα= ab = √3*xx . x>0
c2= a2+b2 => c2= 3x2+x2= 4x2
c= 2x
No to jeszcze jeden sposób ( tylko dla kątów ostrych )
tgα= √3
tgα= ab = √3*xx . x>0
c2= a2+b2 => c2= 3x2+x2= 4x2
c= 2x

 moja "połowica" dzień w dzień przez ponad 35 lat
moja "połowica" dzień w dzień przez ponad 35 lat 


