Zadanko
Godzio: Dla nudzących się

Udowodnić, że dla dowolnych liczb dodatnich a, b, c zachodzi równość:
| 1 | | 1 | | 3 | |
| + |
| ≥ |
| |
| a(1 + b) | | b(1 + c) | | 1 + abc | |
Dawałem je już ale nikt się nie skusił może teraz

?
18 lip 20:03
Godzio: poprawka:
| 1 | | 1 | | 1 | | 3 | |
| + |
| + |
| ≥ |
| |
| a(1 + b) | | b(1 + c) | | c(1 + a) | | 1 + abc | |
18 lip 20:19
Godzio: podpowiem że będzie tu potrzebny fakt że:
średnia arytmetyczna ≥ średnia geometryczna którym
Eta mnie męczyła

18 lip 22:24
Jack:
masakryczna ilość wyrazów mi wychodzi... trzeba się przez nią przedzierać?
19 lip 12:00
Godzio: 6 wyrazów powinno być
19 lip 12:12
Godzio: Rozwiązanie (jeśli dokładnie robione) powinno się zmieścić w 6 linijkach

19 lip 12:13
Jack:
hm to zmienia postać rzeczy − zastanowię się

19 lip 12:20
Godzio: odświeżam

19 lip 21:18
Jack:
Ehh... prawdę mówiąc nie lubię takich zadań, gdzie trzeba robić masę paskudnych obliczeń, a
inny sposób nie przychodzi mi tu do głowy

20 lip 00:29
Godzio: Jutro o 18 napisze rozwiązanie jak nikt nie da rady

a obliczeń naprawdę za dużo nie ma

20 lip 00:48
Franek:

20 lip 00:49
Franek:
No to przed spaniem proste zadanko
Wykaż,że dla a,b >0 spełniajacych warunek ; a
2+b
2= 7ab
zachodzi:
20 lip 01:05
20 lip 01:11
Franek:

Dobranoc

20 lip 01:13
Godzio:
Dobranoc

20 lip 01:14
Franek:
Można też wyjść od danego warunku
a
2+b
2= 7ab
( a+b)
2= 9ab
c.n.u
20 lip 01:18
Godzio: ano można

20 lip 01:22
Basia:
Najprostszy i najbardziej oczywisty jest tutaj dowód nie wprost
a
2+2ab+b
2≠9ab ⇔
a
2+b
2≠7ab
20 lip 04:10
Godzio: Basia co ty tu robisz o tej porze

?
głowisz się może nad moim zadankiem

?
20 lip 04:20
Basia:
A Ty, co tu robiłeś o tej porze ?
20 lip 09:29
Godzio: Nie mogłem zasnąć

20 lip 11:52
Basia:
Ja też, ale mnie więcej o 4:15 jednak mnie senność ogarnęła
20 lip 12:00
bzzz: No Godzio ociupinę zazdroszczę ja mam ostatnio takie dziwne dni, że i na kamieniu bym mogła
zasnąć. Chodząca senność

20 lip 12:02
Godzio: nie ma czego

siedze na kompie i sie nudze albo ewenturalnie w coś pogram
20 lip 12:05
Basia:
Polecam sudoku, ale tylko z miesięcznika "Rozrywka nie tylko sudoku". Tylko tam są na poziomie.
20 lip 12:07
Basia:
Na razie

. Obowiązki wzywają.
20 lip 12:08
bzzz: Basia, są ciekawe, ale z tym poziomem to bym nie przesadzała

bo na poziome są dla mnie z
wydawnictwa press media w książeczce z 4 poziomami trudności, ostatnio te trudne dały mi się
we znaki a do piekielnie trudnych juz mi się odechciało zagladać...
20 lip 12:10
bzzz: Miłego dnia Basiu,


do później
20 lip 12:11
bzzz: Godzio to zapraszam do mnie

mam jeszcze jeden ogródek do oplewienia a czasu i rąk do roboty
brakuje

gwarantuję będziesz spał jak aniołek

20 lip 12:12
Godzio: hah ile płacisz

?
20 lip 12:18
bzzz: a co wizja wyspania się jak człowiek i nie nudzenia się nie jest wystarczającą zachętą

20 lip 12:28
Godzio: hmmm w sumie to ja sie wysypiam bo ide w koncu spac i budze sie o tej 12 (moze nie jak czlowiek
ale zawsze )

takze tylko ta nuda zostaje
20 lip 12:39
Godzio: dobra póki co jade do babci po groszek ( z ogródka

) także żegnam

20 lip 12:41
bzzz: Godzio jesteś inteligentnym człowiekiem

na pewno o ile będziesz chciał znajdziesz sobie
jakieś ciekawe zajęcie, więc skoro do tej pory tego nie zrobiłeś znaczy jedynie, że chcesz się
nudzić

20 lip 12:44
Basia:
Te z Media Press z 4 poziomem trudności starczyły mi na jakieś 4 godziny.
A nie jestem mistrzem Polski.
Wprawdzie to było dwa albo trzy lata temu, może coś się zmieniło. Wtedy się do tego wydawnictwa
skutecznie zniechęciłam i już nigdy go nie kupowałam.
20 lip 12:55
bzzz: wydaje mi się, że ostatnio podnieśli poziom, bo kiedyś też je kupowałam i zaczynałam od razu od
piekielnie trudnych i przeważnie udawało mi się je rozwiązać. Nie wydaje mi się, abym jakimś
dziwnym sposobem nagle zapomniała o jakimś istotnym sposobie rozwiązywania, że nagle sobie z
nimi nie radzę. Bo rozwiązanie typu, że skoro tu mogą być jakieś dwie liczby to podstawmy
jedną z nich i sprawdźmy czy dojdziemy do sprzeczności czy nie, mnie nie interesuje

ja
lubię wstawiać jakąś liczbę kiedy wiem dlaczego tam ma być.
20 lip 12:59
Godzio: Dobra nie będę przedłużać bo widzę że pomysłu brak więc:
Rozwiązanie:
| 1 + abc | | 1 + abc | | 1 + abc | |
| + |
| + |
| ≥ 3 / + 3 |
| a(1 + b) | | b(1 + c) | | c(1 + a) | |
... + 1 + ... + 1 + ... + 1 ? 6
| 1 + abc + a + ab | |
| + ... + ... ≥ 6 |
| a(1 + b) | |
| 1+a | | ab(1+c) | | 1+b | | bc(a+1) | | 1+c | |
| + |
| + |
| + |
| + |
| + |
| a(1+b) | | a(1+b) | | b(1+c) | | b(1+c) | | c(1+a) | |
| 1+a | | b(1+c) | | 1+b | | c(a+1) | | 1+c | | a(b+1) | |
| + |
| + |
| + |
| + |
| + |
| ≥6 |
| a(1+b) | | 1+b | | b(1+c) | | 1+c | | c(1+a) | | 1+a | |
całe wyrażenie dziele przez 6, iloczyn wyrazów po lewej stronie jest równy 1 więc
otrzymuje średnia arytmetyczna ≥ średnia geometryczna c.n.d.
20 lip 14:26
Jack:
niegłupie rozwiązanie...
20 lip 23:05
Godzio: co prawda to prawda
20 lip 23:20
think: 
grunt to skromność co?
20 lip 23:25
Godzio:
hah
ale nie nikt nie powiedział że to moje rozwiązanie

20 lip 23:28
Godzio:
owszem myślałem myślałem i nie wymyśliłem, a jedynie czego nie było w rozwiązaniu to 2 i 4
linijki
20 lip 23:29
think: 
no dobrze już, jednak jesteś gruntownie skromny

20 lip 23:36
Jack:
| | 1 | |
ja kombinowałem żeby rozbić prawą stroną na trzy ułamki |
| i każdy taki odjąć od |
| | 1+abc | |
każdego po lewej stronie... Do czegoś tam doszedłem ale nie widziałem sensu dalszego
rozpisywania...
20 lip 23:37
Godzio: 
Myślałaś że jestem aż tak mądry hehe
20 lip 23:49
think: Godzio, a dlaczego nie?
21 lip 00:02
think: mogę to napisać nawet pogrubionym tekstem. Uważam Godziu, że jesteś mądry
nie twierdzę, że jesteś nieomylny, ale zdaje się, że tacy już się rodzimy
21 lip 00:18
think: 
nie wiem jak wy, ale ja czuję powołanie do wyciągnięcia się pod kołderką

dobrej
nocy wszystkim

21 lip 00:34
Franek:
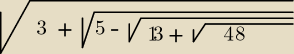
Potwierdzam

i daję zadanie :
wykaż ,że:
21 lip 00:39
21 lip 00:40
Jack:
| | √2(√3+1) | |
√3+√5−√13+√48= |
| /2
|
| | 2 | |
3+
√...=2+
√3 / −3
√5−√13+√48=
√3−1 /
2
5−
√13+√48=3−2
√3+1 / −5
−
√13+√48=−1−2
√3 / : (−1)
√13+√48=1+2
√3 /
2
13+
√48=12+4
√3+1 /−13
√48=4
√3
4
√3=4
√3
21 lip 01:07
Godzio:
| | √6 + √2 | | √2(√3 + 1) | | √2 | | √2 | |
P = |
| = |
| = |
| * (√3+1) = |
| * |
| | 2 | | 2 | | 2 | | 2 | |
√(√3+1)2 =
√24 * (3 + 2√3 + 1) =
√1,5 + √3 + 0,5 =
√2 + √3 =
√3 + √3 − 1 =
√3 + √ 3 − 2√3 + 1 =
√3 + √5 − 1 − 2√3 =
√3 + √5 − √1 + 4√3 + 12 =
p{3 +
√6 − √13 + √48 c.n.d.

21 lip 01:59
Godzio:
chochlik ... = √3 + √5 − √13 + √48
21 lip 01:59
Godzio: Teraz ze spokojnym sumieniem moge iść spać, dobranoc

21 lip 02:00
Franek:
Można też tak:
| | √8+4√3 | |
√3+√5−|1+√12|=√3+√4−2√3=√3+|1−√3|=√2+√3= |
| =
|
| | 2 | |
c.n.d

21 lip 22:33
Godzio: to taki "obcykany" sposób że wzory są pod pierwiastkiem

21 lip 22:49
Franek:

21 lip 22:56
 Udowodnić, że dla dowolnych liczb dodatnich a, b, c zachodzi równość:
Udowodnić, że dla dowolnych liczb dodatnich a, b, c zachodzi równość:
 ?
?





 a obliczeń naprawdę za dużo nie ma
a obliczeń naprawdę za dużo nie ma 

 Dobranoc
Dobranoc 


 ?
głowisz się może nad moim zadankiem
?
głowisz się może nad moim zadankiem  ?
?


 siedze na kompie i sie nudze albo ewenturalnie w coś pogram
siedze na kompie i sie nudze albo ewenturalnie w coś pogram
 . Obowiązki wzywają.
. Obowiązki wzywają.
 bo na poziome są dla mnie z
wydawnictwa press media w książeczce z 4 poziomami trudności, ostatnio te trudne dały mi się
we znaki a do piekielnie trudnych juz mi się odechciało zagladać...
bo na poziome są dla mnie z
wydawnictwa press media w książeczce z 4 poziomami trudności, ostatnio te trudne dały mi się
we znaki a do piekielnie trudnych juz mi się odechciało zagladać...

 do później
do później
 mam jeszcze jeden ogródek do oplewienia a czasu i rąk do roboty
brakuje
mam jeszcze jeden ogródek do oplewienia a czasu i rąk do roboty
brakuje gwarantuję będziesz spał jak aniołek
gwarantuję będziesz spał jak aniołek 
 ?
?

 takze tylko ta nuda zostaje
takze tylko ta nuda zostaje
 ) także żegnam
) także żegnam 
 na pewno o ile będziesz chciał znajdziesz sobie
jakieś ciekawe zajęcie, więc skoro do tej pory tego nie zrobiłeś znaczy jedynie, że chcesz się
nudzić
na pewno o ile będziesz chciał znajdziesz sobie
jakieś ciekawe zajęcie, więc skoro do tej pory tego nie zrobiłeś znaczy jedynie, że chcesz się
nudzić
 ja
lubię wstawiać jakąś liczbę kiedy wiem dlaczego tam ma być.
ja
lubię wstawiać jakąś liczbę kiedy wiem dlaczego tam ma być.
 grunt to skromność co?
grunt to skromność co?

 no dobrze już, jednak jesteś gruntownie skromny
no dobrze już, jednak jesteś gruntownie skromny
 Myślałaś że jestem aż tak mądry hehe
Myślałaś że jestem aż tak mądry hehe
 nie wiem jak wy, ale ja czuję powołanie do wyciągnięcia się pod kołderką
nie wiem jak wy, ale ja czuję powołanie do wyciągnięcia się pod kołderką  dobrej
nocy wszystkim
dobrej
nocy wszystkim 
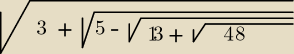 Potwierdzam
Potwierdzam  i daję zadanie :
wykaż ,że:
i daję zadanie :
wykaż ,że:







