Liczby zespolone Gosia: Witam serdecznie, mam problem z zadaniem: Pozpatrzmy liczbę zespoloną z = −1 + i√3 a)oblicz ^z_i−1 b)napisać liczbę zespoloną w postaci trygonometrycznej i obliczyć z⁶ Ostatnio odkryłam tą stronkę i bardzo mi się spodobała, byłabym wdzięczna gdyby ktoś mi udzielił pomocy. Pozdrawiam.

bzzz: ad a)

z		−1+i√3		i+1		−i−1−√3 + i√3
	=		*		=		=
i−1		i−1		i+1		i2 − 1

i(√3 − 1) − 1 − √3		i(1−√3) + 1 + √3
	=
−2		2

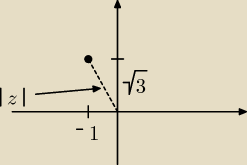
bzzz: co do postaci trygonometrycznej: z = |z|(cosγ + isinγ) ze wzoru de Moivre'a: zⁿ = |z|ⁿ(cosnγ + isinnγ)

Gosia: Dziękuję ślicznie za odpowiedź, jestem bardzo bardzo wdzięczna za pomoc pozdrawiam!

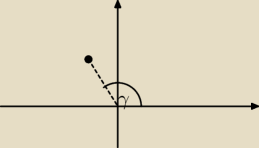
bzzz: zabrakło takiego detalu... Jeżeli chodzi o podpunkt pierwszy i masz podzielić przez liczbę a + bi to zawsze mnożysz licznik i mianownik przez a − bi

AS: ale jeżeli przez liczbę a − bi to mnożysz przez a + bi (licznik i mianownik)

Gosia: Dziękuję!

Kamil: prosze