
 Rozwiązanie znajdujące się na stronie podanej przez bingo wykorzystuje rachunek
pochodnych, który, jak wiemy, nie jest już objęty programem nauczania w szkole średniej.
Spróbujmy więc inaczej i prościej.
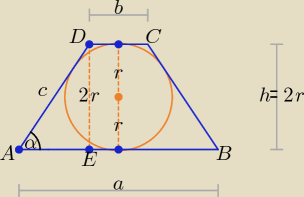
Jeśli czworokąt jest opisany na kole, to korzystając z oznaczeń na załączonym rysunku
Rozwiązanie znajdujące się na stronie podanej przez bingo wykorzystuje rachunek
pochodnych, który, jak wiemy, nie jest już objęty programem nauczania w szkole średniej.
Spróbujmy więc inaczej i prościej.
Jeśli czworokąt jest opisany na kole, to korzystając z oznaczeń na załączonym rysunku
| a + b | ||
mamy: a + b = 2c ⇒ c = | ||
| 2 |
| 2r | 2r | a + b | 2r | |||||
W trójkącie AED: | = sinα ⇒ c = | ⇒ | = | |||||
| c | sinα | 2 | sinα |
| a + b | 2r | 4r2 | ||||
Pole trapezu P = | * 2r = | * 2r = | ||||
| 2 | sinα | sinα |
| 4r2 | ||
Liczba wyrażona wzorem P = | przy danej wartości r jest najmniejsza wtedy, gdy | |
| sinα |



