zada
Kamil: Prosze o pomoc

Wyrazami ciągu (a
n) są kolejne liczby naturalne,które przy dzieleniu przez 6 dają resztę 1.
Ciąg ten jest określony wzorem:
a)a
n=6n−6
b)a
n=6n−5
c)a
n=6n
d)a
n=6n+1
9 lip 18:29
think: zadanie analogiczne do tego, które sam dałeś. Skoro "zrozumiałeś" tłumaczenie Bingo w takim
razie na podstawie tamtego zadania spróbuj rozwiązać to. I bądź tak uprzejmy i nie rozsiewaj
swoich próśb o pomoc w każdym możliwym poście.
9 lip 19:14
Kamil: mozesz patrzec czy dobrze robie ok
9 lip 19:18
Kamil: musi dzielić sie przez 6 i reszta 1
9 lip 19:19
think: mogę.
9 lip 19:19
Kamil: np 7
9 lip 19:21
Kamil: 7 bo dzieli sie przez 6 i reszta 1 dobrze mysle
9 lip 19:21
Kamil: jestes
9 lip 19:22
think: będę aż zrobisz zadanie, więc nie trać czasu mojego i swojego, tylko do dzieła rób zadanie.
9 lip 19:22
Kamil: a dobrze mysle z ta 7
9 lip 19:23
Kamil: nie wiem jak zaczać pomozesz
9 lip 19:24
think: 7 = 6*1 + 1 sam odpowiedz czy dobrze myślisz...
9 lip 19:24
Kamil: prosze
9 lip 19:24
Kamil: czyli dobrze
9 lip 19:25
Kamil: róznica ma pomiedzy wyrazami wynosić 6
9 lip 19:26
Kamil: tak
9 lip 19:26
think: bingo:
Kamil nie płacz a więc mamy tak
3 :4= 0*4 + reszta 3 ... pasuje
7: 4= 1*4+ reszta 3 ... pasuje
11:4= 2*4 + reszta 3 15:4= 3*4 +reszta 3 masz zatem takie liczby:
3, 7, 11, 15, ........ różnica między nimi wynosi 4 czyli tworzą one ciąg arytmetyczny a1= 3 r=
4 wzór na ogólny wyraz ciągu arytmetycznego jest:
an= a1 + ( n−1)*r zatem an= 3+ (n−1)*4
an= 3+4n −4
an= 4n −1
Ty masz policzyć a21 = czyli za n podstawiamy 21
a21= 4*21−1
a21= 84−1= 83
Identyczne zadanie tylko dla innego dzielenia z inną resztą, podobno rozumiałeś rozwiązanie a
wystarczy zrobić analogicznie
9 lip 19:26
Kamil: nie jeste pewien
9 lip 19:26
Kamil: aha
9 lip 19:27
think: tak różnica między wyrazami to 6 tylko jeszcze musisz poprawnie wyznaczyć a1
9 lip 19:27
think: z tą różnicą, że w tym zadaniu polecenie się kończy na wyrazie ogólnym bez liczenia któregoś
tam wyrazu tego ciągu.
9 lip 19:28
Kamil: 7=6*1+1
13=6*2+1
19=6*3+1
25=6*4+1
róznica miedzy nimi wynosi 6
9 lip 19:34
Kamil: zrozumiałem
9 lip 19:35
think: zrozumiałeś, ale brakuje kropeczki nad i

zauważ że od jakiej liczby zaczynało się dzielenie
w zadaniu zrobionym przez Bingo.
9 lip 19:35
Kamil: teraz stosuje wzór ogólny ciagu arytmetycznego
9 lip 19:36
Kamil: gdzie ?
9 lip 19:36
think: 3 linijka ze skopiowanego przeze mnie tekstu
9 lip 19:37
Kamil: mozesz jasnie bo nie wiem o jaka kropeczke ci chodzi nad i
9 lip 19:39
think: chodzi o wszystkie liczby dodatnie, które przy dzieleniu przez 6 dają resztę 1,
jest jeszcze jedna taka liczba przed 7 wiem o niej bo 7>6 póki wyraz ciągu jest większy od
różnicy to istnieje jeszcze przed nim co najmniej jeden wyraz naszego ciągu.
9 lip 19:41
Kamil: napisz ty bo nie widze iii
9 lip 19:42
think: nie czepiałabym się, ale bez tego nie wyznaczysz dobrze a1 a to zmieni Ci wzór na wyraz ogólny
ciągu.
9 lip 19:42
Kamil: przed 6 ci chodzi zebym podał liczbe tak
9 lip 19:43
think: popatrz, żeby od 7 przejść do następnego wyrazu dodajesz 6 i masz 13 a co trzeba zrobić, żeby
poznać wyraz przed 7?
9 lip 19:44
Kamil: powiedz ty bo nie wiem o co ci dokładnie chodzi
9 lip 19:45
Kamil: 5
9 lip 19:45
Kamil: tak
9 lip 19:45
Kamil: 1 to ta iczba tak
9 lip 19:46
Kamil: jestes elo
9 lip 19:46
Kamil: dobrze
9 lip 19:47
Kamil: powiedz cos odezwij sie ok
9 lip 19:47
think:
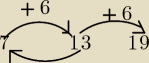
masz rysunek jak idziemy w prawo to dodajemy 6 jak idziemy w lewo to co muszę zrobić aby z 13
otrzymać 7?
9 lip 19:48
Kamil: jestes
9 lip 19:48
Kamil: odjac 6
9 lip 19:48
think: tak 1 to ta liczba, bo
1 = 6*0 + 1
9 lip 19:48
Kamil: to mysle dodrze
9 lip 19:49
Kamil: i co dalej z tym zadaniem?
9 lip 19:49
think: właściwie mógłbyś na podstawie tych zadań wyciągnąć pewien wniosek żeby się z nimi tyle nie
babrać, pierwszy wyraz takiego ciągu to zawsze ta reszta z dzielenia którą podają nam w treści
zadania a r to liczba przez którą dzielimy. przyjrzyj się może to zobaczysz.
9 lip 19:50
think: podaj wzór na ogólny wyraz ciągu arytmetycznego
9 lip 19:50
Kamil: prosze powiedz co dalej?
9 lip 19:50
Kamil: ok
9 lip 19:50
Kamil: an=a1+(n−1)*r
9 lip 19:51
Kamil: no i co dalej?
9 lip 19:52
think: doba, wstaw za a1 i za r to co wyliczyłeś
9 lip 19:52
Kamil: r==6
9 lip 19:53
think: tak a a1 ?
9 lip 19:53
Kamil: a1 nie wiem ile wynosi
9 lip 19:53
think: od jakiej liczby zaczyna się ten ciąg?
9 lip 19:54
Kamil: a1 to ta reszta w zadaniu?
9 lip 19:55
Kamil: od 1
9 lip 19:55
think: to ma być zdanie twierdzące nie pytanie. Ty masz być tego pewien

!
9 lip 19:56
think: w takim razie a1 = 1
podstaw do wzoru i będzie koniec
9 lip 19:56
Kamil: za a1 wstawiamy lczbe które jest na poczatku ciagu czyli od 1
9 lip 19:57
Kamil: zrozumiałem
9 lip 19:58
think: jak zrozumiałeś to bez odbioru jadę na ogród, sam się nie oplewi

9 lip 19:58
Kamil: an=1+(n−1)*6
9 lip 19:59
Kamil: czekaj
9 lip 20:00
Kamil: jestes
9 lip 20:00
Lucyna: a
n = 1 + 6n − 6 = 6n − 5

9 lip 21:03
 Wyrazami ciągu (an) są kolejne liczby naturalne,które przy dzieleniu przez 6 dają resztę 1.
Ciąg ten jest określony wzorem:
a)an=6n−6
b)an=6n−5
c)an=6n
d)an=6n+1
Wyrazami ciągu (an) są kolejne liczby naturalne,które przy dzieleniu przez 6 dają resztę 1.
Ciąg ten jest określony wzorem:
a)an=6n−6
b)an=6n−5
c)an=6n
d)an=6n+1
 zauważ że od jakiej liczby zaczynało się dzielenie
w zadaniu zrobionym przez Bingo.
zauważ że od jakiej liczby zaczynało się dzielenie
w zadaniu zrobionym przez Bingo.
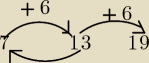 masz rysunek jak idziemy w prawo to dodajemy 6 jak idziemy w lewo to co muszę zrobić aby z 13
otrzymać 7?
masz rysunek jak idziemy w prawo to dodajemy 6 jak idziemy w lewo to co muszę zrobić aby z 13
otrzymać 7?
 !
!

