proste zadania ze statystyki
Mati:
Proszę o pomoc przy tych zadaniach , komenatrz do każdego zadania mile widziany. Wiem , że te
zadania są bardzo proste , mimo to potrzebuje pomocy w ich rozwiązaniu. Każdemu kto się
zainteresuje nimi z góry dziękuje.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Zadanie 1.
Funkcja gęstosci zmiennej losowej X opisana jest wzorem:
| | ⎧ | 3x2 dla 0<=x<=1 | |
| f(x)= | ⎩ | 0 dla pozostałych x |
|
a) narysować wykres funkcji gęstości
b) wyznaczyć dystrybuatnę
c) obliczyć prawdopodobieństwa:
P(X<=
12)
P(
14<=X<
34}
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Zadanie 2.
Zmienna losowa X ma rozkład normalny N(16,2).
a)obliczyc prawdopodobieństwa :
P(X<20)
P(X>=12)
b)wyznaczyć a i b takie, że:
P(X<a)=0,8849
P(X>b)=0,6554
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Zadanie 3.
Dla danych : −0,1 ; 0,15 ; 0,1 ; −0,05 ; oszacować na poziomie ufności 1−α = 0,9
wartość oczekiwaną , przyjmując, że rozkład jest normalny oraz odchylenie standardowe wynosi
0,1.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Zadanie 4.
4. Z populacji o rozkładzie normalnym N(m; 0,1) pobrano próbę trzy elementową :
1,12 ; 1,05 ; 1,13
Na poziomie istotności 0,05 zweryfikować hipotezę , że m=1,20 przeciwko hipotezie H
1 : m >
1,20
Basia:
Zad.2
znormalizować (zestandaryzować) do N(0,1)
P(X<20)=
P(X−16<20−16)=
P(X−16<4)=
to odczytujesz z tablic N(0,1)
pozostałe przykłady tak samo
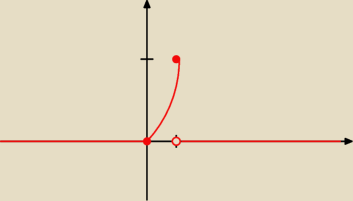Zad.1
dystrubuanta
F(x)= −∞∫x f(t)dt
stąd
dla x≤0
F(x)=−∞∫0dt = C |−∞0 = C−C=0
dla 0<x≤1
F(x) = {−∞∫x f(t)dt = −∞∫0 0dt + 0∫x3t2 dt = 0+t3|0x = x3
dla x>0
F(x) = −∞∫x f(t)dt = −∞∫0 0dt + 0∫13t2 dt+1∫x0 = 0+t3|01+0 = 1
P(X≤x)=F(x)
P(X≤12)=F(12)=(12)3=18
P(14≤X≤34) = P(X≤34)−P(X≤14)=
F(34)−F(14)=(34)3−(14)3 =
2764−164=2664=1332