 a+b+2ca+b=1,5
a+b+2c=1,5a+1,5b
2c = 0,5a+0,5b
c = 14(a+b)
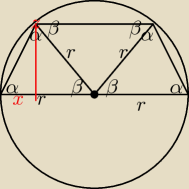
cosα=xc
x=a−b2
a+b+2ca+b=1,5
a+b+2c=1,5a+1,5b
2c = 0,5a+0,5b
c = 14(a+b)
cosα=xc
x=a−b2
| a−b2 | a−b | 4 | 2(a−b) | |||||
cosα= | = | * | = | |||||
| a+b4 | 2 | a+b | a+b |
| b2 | ||
cosβ= | ||
| r |
| b | ||
cosβ= | ||
| 2r |
| 2(2r+2r*cos2α) | ||
cosα= | = | |
| 2r−2r*cos2α |
| 4r(1+cos2α) | |
= | |
| 2r(1−cos2α) |
| 2(1+cos2α) | |
| 1−cos2α |
| −2−2√2 | ||
t1= | =−1−√2 | |
| 2 |
| −2+2√2 | ||
t2= | =−1+√2 | |
| 2 |
 no ja się cykałam, ale w takim razie tak:
a=2r
no ja się cykałam, ale w takim razie tak:
a=2r
| 1 | ||
c= | (a+b)
| |
| 4 |
| 2(a−b) | ||
cosα = | ||
| a+b |
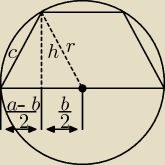
| a−b | ||
c2 = h2 + ( | )2
| |
| 2 |
| b | b2 | |||
r2 = h2 + ( | )2 ⇒ h2 = r2 − | |||
| 2 | 4 |
| 1 | b2 | a−b | ||||
( | (a+b))2 = r2 − | + ( | )2
| |||
| 4 | 4 | 2 |
| 1 | b2 | 2r−b | ||||
( | (2r+b))2 = r2 − | + ( | )2 {pomijam przepisywanie obliczeń, bo nie | |||
| 4 | 4 | 2 |
| 2(a−b) | 2(2r−r(8√2 − 10)) | 3−2√2 | ||||
cosα = | = | = | * | |||
| a+b | 2r + r(8√2 − 10) | √2 − 1 |
| √2+1 | ||
= √2 − 1 | ||
| √2 + 1 |