Zadanko Godzio: Przez punkt P leżący wewnątrz trójkąta ABC poprowadzono proste równoległe do wszystkich boków trójkąta. Pola utworzonych w ten sposób trzech mniejszych trójkątów o wspólnym wierzchołku P wynoszą odpowiednio S₁, S₂, S₃. Obliczyć pole S trójkąta ABC

vega: S(ΔABC) = ( √S₁+√S₂+√S₃)²

Godzio: No dobrze ale jak do tego dojść ?

vega: Zaraz Ci narysuję

Godzio: ok Dzięki

vega:

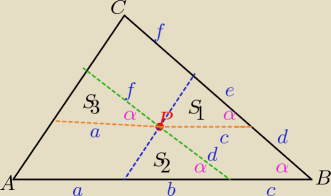
	a
Δ−ty o polach S2 i S3 są podobne w skali k=
	b

to:

	S3		a
		= (		)2
	S2		b

	a		S3
		= √
	b		S2

podobnie Δ−ty o polach: S₁ i S₂ ..... dokończ

	c
ΔABC ~ Δ o polu S2 w skali k=
	b

	a+b+c
k=
	b

	a+b+c
S(ABC) = (		)2*S2=......
	b

dokończ

vega:

	c
Poprawiam zapis: Δ−ty o polach S1 i S2 podobne w slaki k=
	b

	a+b+c
i ΔABC podobny do trójkata o polu S2 w skali k=
	b

Godzio: Dzięki jeszcze raz to już jutro sobie na to popatrzę bo oczy same mi się zamykają Dobranoc

vega: Miłych snów