Zadania różne.
Godzio:
1. Zbadać czy istnieje pochodna funkcji f(x) =
√1 − cosx w punkcie x = 0. Wynik zilustrować
na wykresie funkcji f(x) .
Sprawdziłem i nie istnieje ta pochodna. A ta ilustracja to ma polegać na tym że po prostu to
narysuje bo nie wiem o co z tym chodzi.
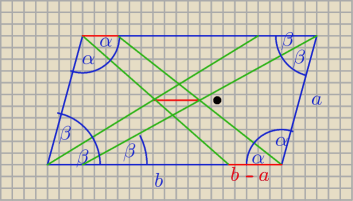
2. Udowodnić, że dwusieczne kątów wewnętrznych równoległoboku tworzą prostokąt, którego
przekątna ma długość równą różnicy długości sąsiednich boków.
2α + 2β = 180
α + β = 90 − jest to prostokąt
I teraz nie mogę dojść do tego że ta dwusieczna jest równoległa do krawędzi, bo wtedy to już
łatwo.
5 lip 19:16
Godzio:
że ta
przekątna jest równoległa do krawędzi ...

5 lip 19:17
Godzio:
3. Ile elementów ma zbiór A jeśli liczba jego podzbiorów trójelementowych jest większa o 48 od
liczby podzbiorów dwuelementowych
| | | | | |
I zrobiłbym to w ten sposób: | − 48 = | |
| | | |
4. Zbadać przebieg zmienności funkcji i narysować wykres funkcji
Tutaj tylko nie wiem jak wyliczyć styczne są na to jakieś sposoby ?
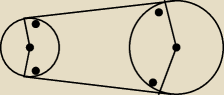
5. Jakiej długości powinien być pas transmisyjny aby można go było użyć do połączenia dwóch kół
o promieniach 20 i 5 cm jeśli odległość środków tych kół wynosi 30 cm
W tym wychodzi mi 30
√3 + 15π a ma być 30
√3 + 30π
Na dzisiaj tyle zadanek

5 lip 19:34
Jack:
1. mozesz policzyć pochodną, potem określić dziedzinę. Okaże się że pochodnej w tym punkcie x=0
nie można policzyć ze względu na dziedzinę własnie. Geomertycznie chodzi o to, że funkcja w
tym punkcie "ostro" zmienia swoją monotoniczność (tzn. nie jest gładka). Możesz też policzyć
pochodne prawo i lewostronne; okaże się że są różne, a więc, że pochodna (obustronna) nie
istnieje.
5 lip 19:36
Jack:
4. współczynnik kierunkowy stycznej do funkcji w punkcie x
0 to pochodna w tym punkcie tej
funkcji. Mając wspólny punkt możesz podać dokładną postać prostej stycznej. Mam nadzieję, że o
to pytasz

5 lip 19:39
Godzio:
a = f'(xo) − to wiem ale jaki jest ten punkt ?
5 lip 19:44
Godzio: 
dlaczego aż 3 Godzie się zrobiły ?
5 lip 20:43
vega:
Może to
"Godzio− trojaczki" ? .....

5 lip 20:57
Basia:
ad.1
to mówi treść zadania; chodzi o x0=0
5 lip 21:33
Basia:
ad.4
podaj dokładną i pełną treść zadania
5 lip 21:35
Basia:
ad.3
oczywiście właśnie tak
5 lip 21:36
Godzio: Chodziło mi o 4

a to już pełna treść

5 lip 21:44
Basia:
ad.2
tam są trójkąty podobne, w których przyprostokątne są odpowiednio równoległe
z tego wynika, że i przeciwprostokątne muszą być równoległe, a to już to o co Ci chodzi
5 lip 21:46
Basia:
ad.4
to nie może być pełna treść
Zbadać przebieg zmienności funkcji i narysować wykres funkcji
jakiej funkcji ?
Tutaj tylko nie wiem jak wyliczyć styczne są na to jakieś sposoby ?
tu w ogóle nie ma mowy o stycznych
5 lip 21:49
Godzio: no tak ale w odpowiedzi są one zawarte
a no tak bo funkcji nie podałem

5 lip 21:52
Godzio: sorki

5 lip 21:52
Basia:
ad.5
jaka Ci wyszła długość odcinka wyciętego ze stycznej przez promienie poprowadzone do punktów
styczności ?
mnie 15
√3
kąt wypukły między promieniami poprowadzonymi do punktów styczności
120 stopni ⇒
pas leży na fragmencie mniejszego okręgu odpowiada kątowi 120 stopni
pas leży na fragmencie większego okręgu odpowiada kątowi 240 stopni
czyli długość pasa = 2*15
√3 +
23*2π*20 +
13*2π*5 =
5 lip 22:05
Godzio:
15
√3 mi tak samo wyszło ale coś się nie wyszło mi z tą długością pasa na kołach skąd wiadomo
że akurat będzie tam 120
o i 240
o ?
5 lip 22:09
Basia:
podaj też pełną odpowiedź; sądzę, że chodzi o coś innego niż o styczne, może o asymptoty, a
może w ogóle jakiś błąd w druku, bo równanie stycznej można napisać tylko w konkretnym punkcie
x0∊D
czasem inaczej formułuje się pytanie
np. w jakim punkcie styczna do krzywej jest równoległa (prostopadła) do danej
lub coś w tym guście
ad.poprzednie
tam ma być oczywiście fragment pasa leżący.....
5 lip 22:10
Basia:
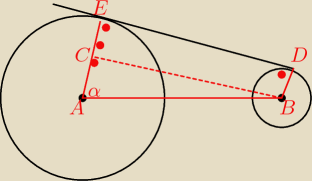
widzisz już ?
BC || DE
|BC|=|DE|=15
√3
|AC|=R−r=15
|AB=30
5 lip 22:15
Godzio: Funkcja parzysta D = ... miejsca zerowe: ... max lok. ... min lok. ....
funkcja rosnąca w ... malejąca w ... wypukła w ... wklęsła w ...punkty przegięcia ...
proste x = −√8 oraz x = √8 styczne do wykresu
5 lip 22:16
Godzio: Teraz już tak dzięki

5 lip 22:16
Basia:
zaraz zobaczę o co tu chodzi
5 lip 22:22
Godzio:
Może wskazówka coś Ci da:
Z postaci dziedziny wynika że funkcja nie może mieć asymptot. Granica lewostronna pochodnej w
punkcie √8 wynosi − ∞ więc prosta x = √8 jest styczna do wykresu funkcji f(x).
5 lip 22:24
Basia:
nie wiem czy ta odpowiedź jest poprawna
w każdym razie na pewno nie istnieje pochodna funkcji w żadnym z tych punktów a
| | f(x)−f(√8) | |
limx→+√8− |
| =−∞ |
| | x−√8 | |
| | f(x)−f(√8) | |
limx→−√8+ |
| =+∞ |
| | x−√8 | |
(do policzenia użyłam reguły de l'Hospitala)
czy to pozwala uznać te proste za styczne nie wiem
5 lip 22:44
Basia:
wskazówkę, jak widzisz, sama sobie napisałam
te ułamki to współczynniki kierunkowe siecznych
dążą do wsp.kierunkowego stycznej
skoro → odpowiednio do −∞ (+∞) to znaczy, że
tgα→ −∞ (+∞) a to znaczy, że
α→ − π2 (π2)
no tak z tego by jednak wynikało, że te proste są stycznymi
5 lip 22:50
Basia:
a w poleceniu po prostu zapomniano napisać "znajdź styczne na końcach przedziału, który jest
dziedziną"
5 lip 22:52
Godzio:
dobra spróbuje to zrozumieć
Dzięki

5 lip 22:56
Basia:
to bardzo specyficzny (i niełatwy) przykład
funkcja jest określona w punktach x=±√8 musi więc istnieć styczna do wykresu w tych punktach
niestety pochodna nie jest w tych punktach określona i nie możemy się nią posłużyć do
wyznaczenia współczynnika kierunkowego (którego zresztą po prostu nie ma bo
tgπ2 i tg−π2 nie istnieją)
posługujemy się więc bezpośrednio definicją i liczymy granicę ilorazu różnicowego w punktach
±√8 odpowiednio prawo i lewostronną i to nas doprowadza do wniosku, że kąt nachylenia → kąta
prostego i styczne muszą mieć taką postać
5 lip 23:00
Godzio: Jutro wrzucę jeszcze trochę zadanek bo je niezbyt rozumiem, także liczę na pomoc

A w środę znów jadę...
5 lip 23:00
Basia:
Jutro gram w brydża, ale Jack i Lucyna pewnie będą, ja zresztą też tak koło 22:00
5 lip 23:03
Godzio: heh, teraz są 2 Jacki i 2 Godzie
5 lip 23:16
Basia:
Widzę 2 Godzie i 1 Jacka.
5 lip 23:36
Basia: No i Eta na pewno będzie, chociaż znowu się ukrywa pod innym nickiem.
5 lip 23:37
Godzio: wcześniej było 2

5 lip 23:37
Jack:
"The best thing about being me... There are so many 'me' s"

Możliwe że wpadnę coby pomóc przy Twoich zadaniach

5 lip 23:43
Godzio:
No ja myśle

startuje o 11 musze się wyrobić z około 20 zadaniami

5 lip 23:45
Basia:
Znowu są dwa Jacki !
Może tak się robi jeżeli wyjdzie się z forum i wróci zanim poprzednie wejście zostało wymazane,
a to zdaje się dopiero po 45 minutach.
5 lip 23:46
Jack:
hoho wcześnie... ale postaram się

5 lip 23:47
Jack:
wiecie co, rozwieje wasze wątpliwości − ja po prostu co jakiś czas zmieniam IP

5 lip 23:48
Godzio: To może póki jesteście to wrzucę zadania ?
Macie ochotę jeszcze porobić

?
5 lip 23:48
Godzio: a no tak ja resetowałem routera i to dlatego

5 lip 23:49
Jack:

Na co czekasz,
Godzio?

5 lip 23:50
Basia:
Wrzucaj, ale może po jednym w każdym poście. Tak łatwiej rozwiązywać i nie mieszają się
odpowiedzi do różnych zadań.
5 lip 23:51
Jack:
Racja.
5 lip 23:52
Godzio: ok już daje
5 lip 23:53
Basia:
A ja nie zmieniam, a mimo to też kiedyś występowałam w trzech osobach.
5 lip 23:53
Lucyna: Basiu zgadza się, będę... pytanie tylko na ile będę przydatna pomimo mojej obecności

ale
Tobie udanego brydża

zazdroszczę Ci, że masz z kim, mnie się niestety nie udało zarazić
nikogo z moich znajomych chęcią do poznania tej gry.
6 lip 10:44
 1. Zbadać czy istnieje pochodna funkcji f(x) = √1 − cosx w punkcie x = 0. Wynik zilustrować
na wykresie funkcji f(x) .
Sprawdziłem i nie istnieje ta pochodna. A ta ilustracja to ma polegać na tym że po prostu to
narysuje bo nie wiem o co z tym chodzi.
2. Udowodnić, że dwusieczne kątów wewnętrznych równoległoboku tworzą prostokąt, którego
przekątna ma długość równą różnicy długości sąsiednich boków.
2α + 2β = 180
α + β = 90 − jest to prostokąt
I teraz nie mogę dojść do tego że ta dwusieczna jest równoległa do krawędzi, bo wtedy to już
łatwo.
1. Zbadać czy istnieje pochodna funkcji f(x) = √1 − cosx w punkcie x = 0. Wynik zilustrować
na wykresie funkcji f(x) .
Sprawdziłem i nie istnieje ta pochodna. A ta ilustracja to ma polegać na tym że po prostu to
narysuje bo nie wiem o co z tym chodzi.
2. Udowodnić, że dwusieczne kątów wewnętrznych równoległoboku tworzą prostokąt, którego
przekątna ma długość równą różnicy długości sąsiednich boków.
2α + 2β = 180
α + β = 90 − jest to prostokąt
I teraz nie mogę dojść do tego że ta dwusieczna jest równoległa do krawędzi, bo wtedy to już
łatwo.



 dlaczego aż 3 Godzie się zrobiły ?
dlaczego aż 3 Godzie się zrobiły ?

 a to już pełna treść
a to już pełna treść


 15√3 mi tak samo wyszło ale coś się nie wyszło mi z tą długością pasa na kołach skąd wiadomo
że akurat będzie tam 120o i 240o ?
15√3 mi tak samo wyszło ale coś się nie wyszło mi z tą długością pasa na kołach skąd wiadomo
że akurat będzie tam 120o i 240o ?
 widzisz już ?
BC || DE
|BC|=|DE|=15√3
|AC|=R−r=15
|AB=30
widzisz już ?
BC || DE
|BC|=|DE|=15√3
|AC|=R−r=15
|AB=30


 A w środę znów jadę...
A w środę znów jadę...

 Możliwe że wpadnę coby pomóc przy Twoich zadaniach
Możliwe że wpadnę coby pomóc przy Twoich zadaniach 
 startuje o 11 musze się wyrobić z około 20 zadaniami
startuje o 11 musze się wyrobić z około 20 zadaniami 


 ?
?

 Na co czekasz, Godzio?
Na co czekasz, Godzio? 
 ale
Tobie udanego brydża
ale
Tobie udanego brydża zazdroszczę Ci, że masz z kim, mnie się niestety nie udało zarazić
nikogo z moich znajomych chęcią do poznania tej gry.
zazdroszczę Ci, że masz z kim, mnie się niestety nie udało zarazić
nikogo z moich znajomych chęcią do poznania tej gry.