wykaż Szprot: Wykaż, ze jeżeli a, b ∊W i a<b, to istnieje taka liczba c∊W, ze a<c<b. Prosze o pomoc!

Jack: np. śr. arytmetyczna

Jack: (pewnie trzeba pokazać jeszcze, że suma l. wymiernych jest wymierna i iloczyn wymiernej przez wymierną też − ale to już jest w miarę proste. Spróbuj zrobić sam, np na forum)

Szprot: jak zapisze c w postaci c=a+b/2 to koniec zadania

Jack: To, że c spełnia a<c<b jest jasne (z wł. średniej arytm. Niemniej też można to pokazać). Być może należy jeszcze pokazać że c∊W... Musisz zapytać nauczyciela, nie wiem czego wymagają od Ciebie

Szprot: móglbyś rozwiazać to zadanie, bo chciałbym poznać sposob rozwiazywania takich zadań

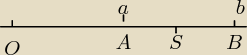
AS: OA = a OB = b AB = b − a

	b − a
Przyjąłem,że S jest środkiem AB , wtedy AS =
	2

	b − a		a + b
OS = OA + AS = a +		=
	2		2

	a + b
Ponieważ S leży między A i B oznacza to,że liczba c =
	2

leży między wartościami a i b.

Szprot: Dzięki. Szacunek

Jack: założmy ze a i b są wymierne.

	p1		p2
Zatem ∃p1,p2,q1≠0,q2≠0 takie, że a=		, b=
	q1		q2

	p1		p2		p1*q2+p2*q1
a+b=		+		=		,
	q1		q2		q1*q2

a+b		p1*q2+p2*q1		c
	=		=		,
2		2q1*q2		d

gdzie c=p₁*q₂+p₂*q₁ oraz d=2q₁*q₂ Można dalej pokazać, że iloczyn l. wymiernych jest wymierny i w ten sposób ostatecznie wykazać,

	c		a+b
że		∊W, a tym samym		.
	d		2

Zadanie sugeruje że trzeba by udowodnić, że c∊W... więc zapisałem szkic takiego dowodu.