ekstrema i punkty przegięcia
Magda: nie wiem czy dobrze mi wyszło, bo trochę dziwne wyniki

to gdyby ktoś mógł sprawdzić:
znaleźć ekstrema i punkty przegięcia funkcji:
mi wyszło tak:
| | 1 | | 1 | |
punkty przegięcia: x=− |
| i x= |
| |
| | √6 | | √6 | |
chyba że coś źle pamiętam i źle liczę

2 lip 22:19
Jack:
hm... ile Ci pochodna wyszła?
2 lip 22:27
Magda: ok, już wiem że się rąbnęłam

to teraz tak mi wyszło:
min: −2
max: 2
hm?
2 lip 22:38
Jack:
pewna jestes? Punkt zero tez powinien Ci wyjść, ponieważ...
f'(x)=x3−4x=x(x2−4)=x(x−2)(x+2)
2 lip 22:44
Magda: damn, nie pamiętam tego. Znaczy wyszło mi tak jak Tobie, tylko teraz muszę sobie przypomnieć
jak to zinterpretować, bo chyba coś źle pamiętam jednak. Ale już czytam coś i powoli mi się
przypomina

dzięki Jack

2 lip 22:53
Jack:
Na razie więcej nie mówię

2 lip 22:55
Magda: ale jestem głuuupia! nie powiem jak to interpretowałam bo to idiotyczne!

czy funkcja może mieć 2 max

bo jeśli tak to max to −2 i 2, a min 0.
teraz dobrze?
2 lip 23:12
Lucyna: a mi wyszło na odwrót...
2 lip 23:13
Lucyna: max w 0 i min w 2 i −2
2 lip 23:13
Jack:
może, ale tu nie ma dwóch max

Zwróć uwagę na znaki w otoczeniu pierwiastka...
2 lip 23:14
Magda: w mordę. a czemu?
2 lip 23:14
Lucyna: Magda, to są maksima i minima lokalne, ta funkcja ogólnie osiąga wartości znacznie większe oraz
znacznie mniejsze, ale te akurat miejsca to są takie zaokrąglone szczyty, gdzie w przypadku
maksimum funkcja traci impet wychamowuje i z części rosnącej przechodzi w majejącą dla minimum
jest odwrotnie.
2 lip 23:15
Jack:
przy x=−2 pochodna zmienia się z "−" na "+" czyli mamy minumum,
przy x=2 podobnie, a przy x=0 z "+" na "−".
2 lip 23:19
Basia:
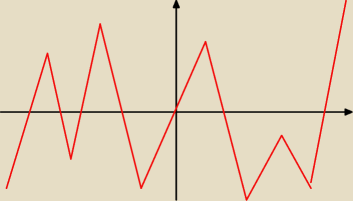
to jest wykres funkcji; ma ona 4 różne maksima i 4 różne minima lokalne
2 lip 23:19
Magda: oki Lucunka, to czaję, ale czemu ma wyjść na odwrót to nie wiem

możecie mi to
łopatologicznie wytłumaczyć?
2 lip 23:21
Lucyna:
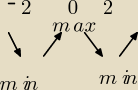
strzałka w dół obrazuje przedział gdzie funkcja jest malejąca strzałka w górę gdzie jest
rosnąca tam gdzie strzałki są bliżej siebie na dole to jest minimum, bliżej siebie na górze,
analogicznie maksimum.
f'(x) = 0 ⇔ x = 0 v x = 2 v x = −2
mamy:
(−∞,−2) dla jakiejś liczby z tego przedziału f'(x) < 0 zatem funkcja tutaj jest malejąca
−2 f'(x) = 0
(−2,0) f'(x) > 0 funkcja jest rosnąca
0 f'(x) = 0
(0,2) f'(x) < 0 f.malejąca
2 f'(x) = 0
(2,∞) f'(x) > 0 f.rosnąca
2 lip 23:22
Jack:
napisałem Ci − zależy od zmiany znaków w otoczeniu tego punktu we wzorze pochodnej...
2 lip 23:23
Jack:
ooo

2 lip 23:23
Basia:
f'(x)=x(x−2)(x+2)
określ znak pochodnej w przedziałach:
(−∞,−2)
(−2,0)
(0,2)
(2,+∞)
tam gdzie pochodna jest dodatnia tam funkcja rośnie
tam gdzie pochodna jest ujemna tam funkcja maleje
jeżeli najpierw rośnie a potem maleje masz maksimum
jeżeli najpierw maleje a potem rośnie masz minimum
2 lip 23:26
Magda: ło matko

ale się fajnie wczuliście

tylko mi nie o to chodzi

bo ja nie czaiłam czemu w przedziałach (−
∞,−2) i (0,2) Wam wyszło że jest mniejsze od zera a w
tamtych że jest większa

to że jak najpierw rośnie potem maleje to jest max i na odwrót to
wiem

Ale teraz już WSZYSTKO rozumiem

sorry

ale na prawdę bardzo mi miło że się tak staracie

!

2 lip 23:33
Lucyna: jak Ci zależy możemy przestać

specjalnie zaczniemy robić błędy, zdaje się, że szukanie u
kogoś błędów ma niezłe działanie na zapamiętanie materiału

2 lip 23:47
Lucyna: no dobra wy tu dzielnie pracujcie dalej ja idę się oddać uciechom

może z jeden
rozdział
mi się uda przeczytać zanim padnę

dobrej nocy wszystkim.
3 lip 00:01
Basia:
Też kończę. Dobranoc i kolorowych snów.
3 lip 00:04
Magda: dobranoc dziewczynki

3 lip 00:14
 to gdyby ktoś mógł sprawdzić:
znaleźć ekstrema i punkty przegięcia funkcji:
to gdyby ktoś mógł sprawdzić:
znaleźć ekstrema i punkty przegięcia funkcji:

 to teraz tak mi wyszło:
min: −2
max: 2
to teraz tak mi wyszło:
min: −2
max: 2
 dzięki Jack
dzięki Jack 

 czy funkcja może mieć 2 max
czy funkcja może mieć 2 max bo jeśli tak to max to −2 i 2, a min 0.
teraz dobrze?
bo jeśli tak to max to −2 i 2, a min 0.
teraz dobrze?
 Zwróć uwagę na znaki w otoczeniu pierwiastka...
Zwróć uwagę na znaki w otoczeniu pierwiastka...
 to jest wykres funkcji; ma ona 4 różne maksima i 4 różne minima lokalne
to jest wykres funkcji; ma ona 4 różne maksima i 4 różne minima lokalne
 możecie mi to
łopatologicznie wytłumaczyć?
możecie mi to
łopatologicznie wytłumaczyć?
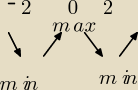 strzałka w dół obrazuje przedział gdzie funkcja jest malejąca strzałka w górę gdzie jest
rosnąca tam gdzie strzałki są bliżej siebie na dole to jest minimum, bliżej siebie na górze,
analogicznie maksimum.
f'(x) = 0 ⇔ x = 0 v x = 2 v x = −2
mamy:
(−∞,−2) dla jakiejś liczby z tego przedziału f'(x) < 0 zatem funkcja tutaj jest malejąca
−2 f'(x) = 0
(−2,0) f'(x) > 0 funkcja jest rosnąca
0 f'(x) = 0
(0,2) f'(x) < 0 f.malejąca
2 f'(x) = 0
(2,∞) f'(x) > 0 f.rosnąca
strzałka w dół obrazuje przedział gdzie funkcja jest malejąca strzałka w górę gdzie jest
rosnąca tam gdzie strzałki są bliżej siebie na dole to jest minimum, bliżej siebie na górze,
analogicznie maksimum.
f'(x) = 0 ⇔ x = 0 v x = 2 v x = −2
mamy:
(−∞,−2) dla jakiejś liczby z tego przedziału f'(x) < 0 zatem funkcja tutaj jest malejąca
−2 f'(x) = 0
(−2,0) f'(x) > 0 funkcja jest rosnąca
0 f'(x) = 0
(0,2) f'(x) < 0 f.malejąca
2 f'(x) = 0
(2,∞) f'(x) > 0 f.rosnąca

 ale się fajnie wczuliście
ale się fajnie wczuliście  tylko mi nie o to chodzi
tylko mi nie o to chodzi  bo ja nie czaiłam czemu w przedziałach (−∞,−2) i (0,2) Wam wyszło że jest mniejsze od zera a w
tamtych że jest większa
bo ja nie czaiłam czemu w przedziałach (−∞,−2) i (0,2) Wam wyszło że jest mniejsze od zera a w
tamtych że jest większa  to że jak najpierw rośnie potem maleje to jest max i na odwrót to
wiem
to że jak najpierw rośnie potem maleje to jest max i na odwrót to
wiem Ale teraz już WSZYSTKO rozumiem
Ale teraz już WSZYSTKO rozumiem  sorry
sorry ale na prawdę bardzo mi miło że się tak staracie
ale na prawdę bardzo mi miło że się tak staracie !
! 
 specjalnie zaczniemy robić błędy, zdaje się, że szukanie u
kogoś błędów ma niezłe działanie na zapamiętanie materiału
specjalnie zaczniemy robić błędy, zdaje się, że szukanie u
kogoś błędów ma niezłe działanie na zapamiętanie materiału
 może z jeden
rozdział
mi się uda przeczytać zanim padnę
może z jeden
rozdział
mi się uda przeczytać zanim padnę  dobrej nocy wszystkim.
dobrej nocy wszystkim.
