| 643 | ||
a) jest rowne | b) jest liczbą całkowitą c) jest równe 642*643
| |
| 2 |
| 643*642 | ||
d) jest równe | ||
| 2 |
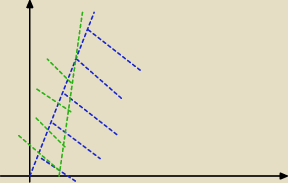 niebieskim kolorem zaznaczyłam płaszczyznę y ≤ 642x
zielonym natomiast płaszczyznę y ≥ 643(x−1)
interesuje nas punkt przecięcia prostych y=642x z y=643(x−1) ponieważ już na rysunku widać, że
interesujący nas obszar to trójkąt, potrzebna nam jego wysokość, oraz długość podstawy.
Wysokość, to y, który wyjdzie z rozwiązania powyższego układu równań.
Teraz podstawa to długość odcinka (x1,0) (x2,0)
(x1) 0 = 642x1 ⇒ x1 = 0
(x2) 0 = 643(x2−1) ⇒ x2 = 1
Długość odcinka od (0,0) do (0,1) to 1.
Zatem nasz trójkąt ma podstawę o długości 1, oraz wysokość h = ...
Pole trójkąta to P = ah2 wylicz h a poznasz prawidłową odpowiedź
niebieskim kolorem zaznaczyłam płaszczyznę y ≤ 642x
zielonym natomiast płaszczyznę y ≥ 643(x−1)
interesuje nas punkt przecięcia prostych y=642x z y=643(x−1) ponieważ już na rysunku widać, że
interesujący nas obszar to trójkąt, potrzebna nam jego wysokość, oraz długość podstawy.
Wysokość, to y, który wyjdzie z rozwiązania powyższego układu równań.
Teraz podstawa to długość odcinka (x1,0) (x2,0)
(x1) 0 = 642x1 ⇒ x1 = 0
(x2) 0 = 643(x2−1) ⇒ x2 = 1
Długość odcinka od (0,0) do (0,1) to 1.
Zatem nasz trójkąt ma podstawę o długości 1, oraz wysokość h = ...
Pole trójkąta to P = ah2 wylicz h a poznasz prawidłową odpowiedź
