bfnm,m
cherry: Kąt BAC trójkąta ABC ma miarę 13 stopni, a kat ACB miarę 119stopni. Wysokość CD dzieli bok AB
na dwa odcinki, z których krótszy ma długość 25 cm. Oblicz długość boku AC.
30 cze 19:09
Basia:
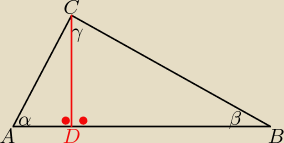
β=13
γ=119
α=180−119−13=48
|AD=25
cos48 znajdź w tablicach i wykonaj rachunki
30 cze 19:17
cherry: dzięki wielkie

30 cze 19:19
Basia:
oj źle przeczytałam te kąty
α=13
γ=119
β=48
z tego wynika, że krótszy będzie |BD|=25
czyli
teraz trzeba zastosować tw.sinusów
30 cze 19:38
cherry: Oh, no tak, dzięki jeszcze raz

30 cze 20:00
NyiiLee: Wyjdzie 75, ale w odpowiedziach widnieje wynik 123,4 cm. Czy ktos jest w stanie mi wytlumaczyc
why?!
20 lut 19:28
Martaa: Od kiedy na maturze można sprawdzać coś w tablicach?
5 mar 14:29
DAmcio: Zadanie w kiełbasie jest na poziomie podstawowym a tw sinusow sa na rozszerzeniu wiec jest
pewnie prostsza metoda

7 kwi 18:14
wojtek: @NyiiLee Dobrze wyszło. Faktycznie musi być inny sposób, bo zadanie jest oznaczone jako
podstawowe, no chyba że Andrew Sausage się machnął.
14 kwi 20:22
Kasia: W odpowiedsi jest dobrze
Należy :
W trójkącie DBC. CD/25 = tg 48
Z tego wyliczyć CD i nastepnie w trójkącie ADC CD/AC = sin 13
CD/25= tg48
CD =27.765
CD/AD = sin13
AD = CD/sin13 = 123.4
5 mar 13:33
aniabb: Na maturze sprawdzać w tablicach można było zawsze ... a od bodajże 15 lat tablice masz nawet
na ławce
5 mar 14:09
aniabb: ooo to pytanie sprzed 5 lat...ale odkopali temat

5 mar 14:10
 β=13
γ=119
α=180−119−13=48
|AD=25
β=13
γ=119
α=180−119−13=48
|AD=25



