oblicz całkę desperat: ∫|x|

Basia: hm........ a na pewno ma być nieoznaczona ?

desperat: to jest z zadania z zastosowania całki (obliczanie pola pod wykresem ) i no faktycznie przy tym będzie to całka oznaczona a zadanie wygada tak : podane są 3 funkcje y=|x| y=x=2 x=2 i należy obliczyć pole między z wykresami i tu właśnie pojawia się problem obliczenia całki z modułu

Basia: ale to zupełnie co innego i da się zrobić, zaraz napiszę jak

Basia: ale najpierw popraw wzór drugiej funkcji y=x+2 ma być czy y=x−2 ?

desperat: y=x+2 przepraszam

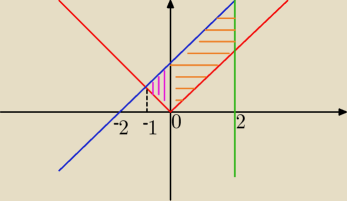
Basia: P = P₁+P₂ P₁ = ∫₋₁⁰ [(x+2)−|x|]dx = ∫₋₁⁰ [(x+2)−(−x)]dx = ∫₋₁⁰ [2x+2]dx bo w przedziale <−1,0> |x|=−x P₂ =∫₀² [(x+2)−|x|]dx = ∫₀² [x+2−x]dx = ∫₀² 2dx bo w przedziale <0,2> |x|=x teraz już sobie chyba poradzisz

desperat: dzięki wielkie myślę że dam już sobie z tym rade ale czy mogłabyś mi jeszcze wytłumaczyć dlaczego mimo modułu bierzemy −x kiedy to wiemy ze jest raz ujemne a raz dodatnie czy to zależy w tym przypadku od wykresu

Basia: |−2|=2=−(−2) |−3|=3=−(−3) |2|=2 |3|=3 −x dla x<0 |x| = x dla x≥0 to jest definicja modułu

desperat: a moglabyś mi jeszcze dla utrwalenia rozwiązać takie pole że : y=|x| y=x−2 bo my troche inaczej to liczymy w sensie takim że liczymy najpierw pole całości a później odejmujemy zbędne części

Basia: 1. czegoś tam brakuje, ten obszar jest nieograniczony 2. nie ma różnicy; liczy się tak jak akurat jest najwygodniej

Basia: tamto poprzednie liczone Twoją metodą to: ∫₋₂² (x+2) dx − ∫₋₁⁰|x| dx − ∫₀²|x| dx = ∫₋₂² (x+2) dx − ∫₋₁⁰(−x) dx − ∫₀²x dx = ∫₋₂² (x+2) dx + ∫₋₁⁰x dx − ∫₀²x dx

Basia: oj błąd to jest ∫₋₁²(x+2)dx − ∫₋₁⁰ |x| dx − ∫₀² |x| dx = ∫₋₁²(x+2)dx − ∫₋₁⁰ (−x) dx − ∫₀² x dx = ∫₋₁²(x+2)dx + ∫₋₁⁰ x dx − ∫₀² x dx

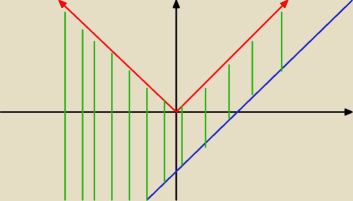
Basia: pole tego obszaru jest z całą pewnością nieskończenie duże