HELP ;] Amaz: Pomóżcie proszę http://www.math.uni.wroc.pl/~newelski/dydaktyka/wdm-A/listy/lista4b.pdf Chodzi o zadanie drugie przykład a Wg mnie nie jest możliwe, aby zbiór A i B były rozłączne, czy mam rację?

Amaz: wg mnie te zbiory są wręcz sobie równe, być może źle to rozumiem...

Amaz: Może nie do końca wiecie co to jest π_x[A] Rozważmy teraz zbiór A⊆ X x Y. Rzutem zbioru A na pierwszą oś nazywamy zbiór pierwszych współrzędnych par <x,y> należących do zbioru A. Oznaczamy go przez π_x[A]. Analogicznie jest z π_Y[A] Kierując się tymi definicjami w zadaniu2 w przykładzie a) wychodzi mi, że zbiór A=B, ale nie chce mi się wierzyć, że to jest aż tak banalne...

Amaz: halp

Lucyna: ale jak ma się do Twojego wyniku warunek, że A i B mają być rozłączne

Amaz: no wlasnie wychodzi na to, że ja chyba nie rozumiem tego zadania... tzn tego podpunktu, bo (b) i (c) umiem

Amaz: no bo jak A i B mają być rozłączne skoro π_X[A]=π_X[B]=[¹₄,³₄]=π_Y[A]=π_Y[B]

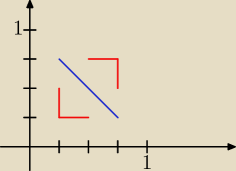
Lucyna: proponuję takie zbiory

Amaz: aaa dzięki, ja nie mogłem tego skumać, dzięki wielkie! Bo ja się uparłem, że zbiory A i B muszą być jakimiś kwadratami, nie wziąłem czegos takiego pod uwage, teraz już wszystko wiem

Lucyna: No mam tylko nadzieję, że to jest dobrze

Amaz: No jest napewno dobrze, bo te rzuty się zgadzają

Lucyna: raczej więcej Ci nie pomogę, bo ja ten przedmiot nazywałam wstrętem do matematyki