Mateusz:
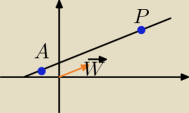
Prostą mozna dosyc łatwo przedstawic w postaci parametrycznej wystarczy tylko zauwazyc ze punkt
A na rysunku i niezerowy wektor w wyznaczają prostą −przechodzącą przez A i równoległą do
wektora w dla kazdego punktu P na tej prostej mamy
→
AP = t*w gdzie t Є R i teraz gdy przejdziemy do wspołrzędnych A = (x
0,y
0),P=(x,y) i
→ → →
w =[w
1,w
2] AP =[x−x
0 y−y
0]=t*w = t*[w
1 w
2]=[t*w
1 t*w
2]
x−x
0 = t*w
1 y−y
0 = t*w
2 i tak oto mamy przedstawienie parametryczne prostej
(w
1*t+x
0,w
2*t+y
0) oraz rownania parametryczne
{x = w
1*t+x
0 t ЄR
{y = w
2*t+y
0
z góry dziekuje