zadanie - nierówność kwadratowa z ** gerwazy: Wyznacz te wartsości parametru m(m∊R), dla których oba rozwiązania równania mx²−(m²+m+1)x+m+1=0 są większe od 1. założenia jakie rozpisałem a≠0 czyli m≠0 Δ≥0 x_w>1 a*f₁>0 dobrze rozpisane? Δ mam obliczoną, bo była we wskazówkach, jest też, że m≠0, ale nie wiem czy to odpowiedź czy coś do wskazówki, ale przecież nie dzieliliśmy przez m nigdzie więc chyba odpowiedź z góry dziękuję za odpowiedź

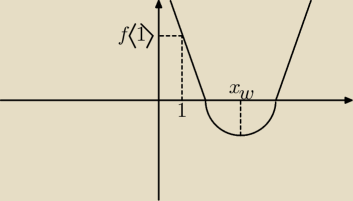
Godzio: mx² − (m² + m + 1)x + m + 1 = 0 m ≠ 0 − żeby w ogóle była to funkcja kwadratowa f(1) > 1 − tak jak wynika z rysunku Δ ≥ 0 − istnienie 2 rozwiązań (niekoniecznie różnych) x_w > 1 − to także wynika z rysunku x_w > 1 } Te 2 warunki wskazują że miejsca zerowe są większe od jedynki f(1) > 1 }

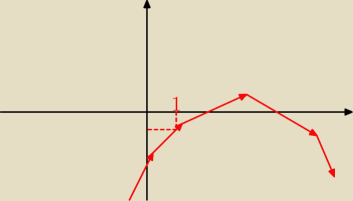
Basia: Godzio f(1) jak widać na załączonym pokracznym obrazku nie musi być dodatnie: 1. Δ>0 2. x_w>1 3. a>0 i f(1)>0 lub a<0 i f(1)<0 ⇔ a*f(1)>0

Godzio: też prawda

Godzio: ale też dopowiem: Δ ≥ 0 bo nie ma w poleceniu różnych rozwiązań

Basia: a to już kwestia interpretacji; przez "oba rozwiązania" rozumiałabym jednak dwa różne, ale zgadzam się, że polecenie nie jest precyzyjne