nierownosci wielomianowe
oliwia:
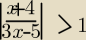
hej. jak rozwiazujemy nierownosci wymierne z wartosci bezwzgledna typu
19 cze 18:50
Kejt:
| x+4 | | x+4 | |
| >1 v |
| <−1 |
| 3x−5 | | 3x−5 | |
19 cze 18:51
malibu:
| | 5 | |
przy założeniu : 3x−5 ≠0 => x ≠ |
| |
| | 3 | |
19 cze 18:54
oliwia: a dziedzina jakas jest?
19 cze 18:54
oliwia: aha czyli jak wyjdzie mi to ma to byc suma wyniku z dziedzina czy czesc wspolna?
19 cze 18:55
oliwia: prosze o odp
19 cze 19:04
oliwia: czesc wspoln?
19 cze 19:14
oliwia: powiedzcie
19 cze 19:36
Lucyna: część wspólna, pomyśl chwilkę.
Jeśli suma... to np wyszły Ci rozwiązania 3,5,7 a dziedzina to {2,4,5,6} to przecież nie możesz
za rozwiązanie podać punktów dla których funkcja jest nieokreślona.
19 cze 19:46
Lucyna: sumuje się tylko rozwiązania z poszczególnych przypadków, masz dwa przypadki. Masz wziąć sumę
rozwiązań, czyli rozwiązania z 1 przypadku plus rozwiązania z 2 przypadku a następnie, część
wspólną z dziedziną.
19 cze 19:48
oliwia: dziekuje
19 cze 19:50
oliwia: chcialam zapytac... bo mam problem.. dlaczgeo w niektorych zadaniach jezeli zalozenie jest ze
xrozne od 2 to pomimo tego w rozwiazaniu bieremy pod uwage to 2 a w innych nie. np.
| x2−5x+4x2−4|≥1 i rozwiazanie wychodzi (−∞, −2)∪(−2,o>∪<8/5,2)∪(2,5/2>
a tu jest inaczej
|2x−5x+1|≤2 i tu wycjsc powinno <3/4 , +∞)
19 cze 21:32
Lucyna: 
ponieważ tam gdzie są nawiasy typu () to są tzw przedziały otwarte, czyli bez tych punktów
koło których jest ten nawias np przedział (−∞,3) oznacza że mamy zbiór od minus
nieskończoności do trzech, ale bez trójki. Wynika to z tego, że jest niemożliwe podanie punktu
mniejszego od trzech, bo zawsze można wskazać jeszcze mniejszy. Powiesz 2,99 ktoś będzie
bardziej precyzyjny powie 2,99999 ale tak można się bawić w nieskończoność, dlatego przyjęła
się taka właśnie konwencja. Natomiast gdy chcemy zaznaczyć, że do przedziału należy jakiś
punkt stawiamy nawiasy <> tzw. zamknięte, oczywiście mogą być przedziały lewostronnie otwarte
a prawostronnie domknięte lub na odwrót.
20 cze 00:39
oliwia: nie wiem czy zauwazylas ale oba przedzialy sa tutaj domkniete
20 cze 05:34
oliwia: tzn funkcje maa znaki ≤ lub≥
20 cze 08:52
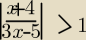 hej. jak rozwiazujemy nierownosci wymierne z wartosci bezwzgledna typu
hej. jak rozwiazujemy nierownosci wymierne z wartosci bezwzgledna typu
 ponieważ tam gdzie są nawiasy typu () to są tzw przedziały otwarte, czyli bez tych punktów
koło których jest ten nawias np przedział (−∞,3) oznacza że mamy zbiór od minus
nieskończoności do trzech, ale bez trójki. Wynika to z tego, że jest niemożliwe podanie punktu
mniejszego od trzech, bo zawsze można wskazać jeszcze mniejszy. Powiesz 2,99 ktoś będzie
bardziej precyzyjny powie 2,99999 ale tak można się bawić w nieskończoność, dlatego przyjęła
się taka właśnie konwencja. Natomiast gdy chcemy zaznaczyć, że do przedziału należy jakiś
punkt stawiamy nawiasy <> tzw. zamknięte, oczywiście mogą być przedziały lewostronnie otwarte
a prawostronnie domknięte lub na odwrót.
ponieważ tam gdzie są nawiasy typu () to są tzw przedziały otwarte, czyli bez tych punktów
koło których jest ten nawias np przedział (−∞,3) oznacza że mamy zbiór od minus
nieskończoności do trzech, ale bez trójki. Wynika to z tego, że jest niemożliwe podanie punktu
mniejszego od trzech, bo zawsze można wskazać jeszcze mniejszy. Powiesz 2,99 ktoś będzie
bardziej precyzyjny powie 2,99999 ale tak można się bawić w nieskończoność, dlatego przyjęła
się taka właśnie konwencja. Natomiast gdy chcemy zaznaczyć, że do przedziału należy jakiś
punkt stawiamy nawiasy <> tzw. zamknięte, oczywiście mogą być przedziały lewostronnie otwarte
a prawostronnie domknięte lub na odwrót.