 Kolejne zadanko do sprawdzenia:
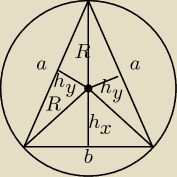
Wśród trójkątów równoramiennych wpisanych w koło o promieniu znaleźć ten, który ma największe
pole.
h = 2hy + hx = hx + R
2hy = R
Kolejne zadanko do sprawdzenia:
Wśród trójkątów równoramiennych wpisanych w koło o promieniu znaleźć ten, który ma największe
pole.
h = 2hy + hx = hx + R
2hy = R
| R | ||
hy = | ||
| 2 |
| 1 | ||
R2 − hy2 = | a2 | |
| 4 |
| 1 | ||
(R+hx)2 + | b2 = a2 | |
| 4 |
| 1 | ||
hx2 + | b2 = R2 − | |
| 4 |
| R2 | R | |||
hx = | = | |||
| 2R | 2 |
| 1 | ||
hx2 + | b2 = R2 | |
| 4 |
| b*h | R√3 * 1,5R | 3 | ||||
P = | = | = | R2√3 | |||
| 2 | 2 | 4 |




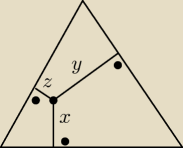 h = 2hy + hx − wzięło się z tego, że jest takie coś że odcinki łączące dowolny punkt w
trójkącie z bokami (pod kątem prostym) są równe wysokości x + y + z = h
a ta wysokość to zawsze dzieli na pół w równoramiennym
h = 2hy + hx − wzięło się z tego, że jest takie coś że odcinki łączące dowolny punkt w
trójkącie z bokami (pod kątem prostym) są równe wysokości x + y + z = h
a ta wysokość to zawsze dzieli na pół w równoramiennym 

 Ja liczę tak :
γ −−kąt między ramionami γ €(0, 180)
Ja liczę tak :
γ −−kąt między ramionami γ €(0, 180)
| R2*sin2γ | R2*sin( 180o−γ) | |||
P= | + 2* | |||
| 2 | 2 |
| a√3 | ||
R= | ||
| 3 |
| 3R2√3 | ||
P= | ||
| 4 |

 Może cokolwiek rozumiem,
P'(γ) = 0 −> to jest wyznaczanie ekstremum lokalnych tak ?
Może cokolwiek rozumiem,
P'(γ) = 0 −> to jest wyznaczanie ekstremum lokalnych tak ?




 Witam.
Najpierw wyjaśnienie.
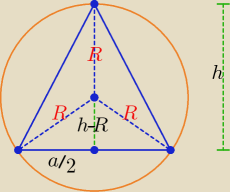
Suma odległości od boków trójkąta punktu leżącego wewnątrz tego trójkąta jest równa długości
wysokości tego trójkąta − to twierdzenie dotyczy tylko trójkąta równobocznego.
Nie można tutaj zastosować tego twierdzenia.
Rozwiązanie.
Witam.
Najpierw wyjaśnienie.
Suma odległości od boków trójkąta punktu leżącego wewnątrz tego trójkąta jest równa długości
wysokości tego trójkąta − to twierdzenie dotyczy tylko trójkąta równobocznego.
Nie można tutaj zastosować tego twierdzenia.
Rozwiązanie.
| a2 | ||
(h − R)2 + | = R2 ⇒ a = 2√ 2hR − h2 , a > 0, h > 0, R > 0 | |
| 4 |
| 1 | 1 | |||
Pole P = | ah = | h*2√ 2hR − h2 ⇒ P(h) = √ 2Rh3 − h4 | ||
| 2 | 2 |
| 6Rh2 − 4h3 |
| ||||||||||||
P'(h) = | = | . | |||||||||||
| 2√Rh3 − h2 | 2√Rh3 − h2 |
| 3 | ||
Funkcja P(h) posiada maksimum dla h = | R i a = 2√ 2hR − h2 = R√3 | |
| 2 |
| 1 | 1 | 3 | 3 | |||||
P = | ah = | *R√3* | R = | R2√3 | ||||
| 2 | 2 | 2 | 4 |


| 6Rh2 − 4h3 | ||
P'(h) = | ? | |
| 2√Rh3 − h4 |
 , dziękuję za dostrzeżenie błędnego zapisu.
, dziękuję za dostrzeżenie błędnego zapisu.

 α+β+γ= 180o
α+β+γ= 180o
| abc | ||
P= | ||
| 4R |
| 3√3 | ||
max wyrażenia sin360o= | ||
| 8 |
| 3√3 | ||
P= | R2 | |
| 4 |
 Muszę kończyć ( idę na grila)
pozdrawiam
Muszę kończyć ( idę na grila)
pozdrawiam 

| α+β | β+γ | γ+α | ||||
cosα + cosβ + cosγ = 4cos | cos | cos | ||||
| 2 | 2 | 2 |
| α+β | ||
x = | => 2x = α + β | |
| 2 |
| β+γ | ||
y = | => 2y = β + γ | |
| 2 |
| γ+α | ||
z = | => 2z = γ + α | |
| 2 |
 a ja znam rozwiązanie
a ja znam rozwiązanie 
 ale jestem z siebie dumna!
ale jestem z siebie dumna!
| α+β | β+γ | γ+α | ||||
4cos | cos | cos | = {podstawiamy za γ = 90−α−β} | |||
| 2 | 2 | 2 |
| α+β | β+90−α−β | 90−α−β+α | ||||
4cos | cos | cos | ||||
| 2 | 2 | 2 |
| 1 | ||
= {korzystamy ze wzoru cosαcosβ = | [cos(α+β) + cos(α−β)]} =
| |
| 2 |
| α+β | 1 | α+β | 1 | β−α | α+β | α+β | ||||||||
4cos | ( | cos(90− | + | cos | ) = 2cos | cos(90− | ) + | |||||||
| 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| α+β | β−α | |||
2cos | cos | |||
| 2 | 2 |
| 1 | ||
= {ponownie ten sam wzór cosαcosβ = | [cos(α+β) + cos(α−β)]} =
| |
| 2 |
| 1 | 1 | |||
2* | (cos90 + cos(α+β−90)) +2* | (cosβ + cosα) = cos(−γ) + cosα + cosβ = cosα + cosβ + | ||
| 2 | 2 |






 trzeba się wyspać, żeby przez pomyłkę nie oddać głosu na nie tego
kandydata
trzeba się wyspać, żeby przez pomyłkę nie oddać głosu na nie tego
kandydata
 a+b+c= 90o cos90o=0
cosa+cosb +cosc= (cosa+cosb) + ( cosc+ cos(a+b+c)]=
a+b+c= 90o cos90o=0
cosa+cosb +cosc= (cosa+cosb) + ( cosc+ cos(a+b+c)]=
| −a−b | a+b | |||
cos | = cos | −−− z parzystości cosinusa
| ||
| 2 | 2 |
| a+b | a−b | 2c+a+b | a+b | |||||
2cos | *cos | + 2cos | *cos | =
| ||||
| 2 | 2 | 2 | 2 |
| a+b | a−b | 2c+a+b | ||||
2cos | ( cos | + cos | )=
| |||
| 2 | 2 | 2 |
| a+b | a+c | b+c | ||||
2cos | *2cos | *cos | ||||
| 2 | 2 | 2 |
| a+b | a+c | b+c | ||||
= 4 cos | *cos | *cos | ||||
| 2 | 2 | 2 |

 Sposobów wykazania prawdziwości podanej przez Godzia równości trygonometrycznej
jest więcej. Pokażę jeszcze jeden dowód, jest on mniej elegancki od dowodu Ety.
_______________________________________________________________________
α + β + γ = 90o, α = 900 − β − γ, β = 900 − α − γ, γ = 900 − α − β.
_______________________________________________________________________
Sposobów wykazania prawdziwości podanej przez Godzia równości trygonometrycznej
jest więcej. Pokażę jeszcze jeden dowód, jest on mniej elegancki od dowodu Ety.
_______________________________________________________________________
α + β + γ = 90o, α = 900 − β − γ, β = 900 − α − γ, γ = 900 − α − β.
_______________________________________________________________________
| α + β | α + β | α + β | ||||
cosγ = cos(90o − (α + β)) = sin(α + β) = sin2* | = 2sin | cos | = | |||
| 2 | 2 | 2 |
| α + β | α + β | 180o − α − β | α + β | |||||
= 2cos(90o − | )cos | = 2cos | cos | = | ||||
| 2 | 2 | 2 | 2 |
| 90o + γ | α + β | |||
= 2cos | cos | . | ||
| 2 | 2 |
| α + β | α − β | 90o + γ | α + β | |||||
cosα + cosβ + cosγ = 2cos | cos | + 2cos | cos | = | ||||
| 2 | 2 | 2 | 2 |
| α + β | α − β | 90o + γ | ||||
= 2cos | (cos | + cos | ) = | |||
| 2 | 2 | 2 |
| α + β |
|
| ||||||||||||||||||||||
= 2cos | *2cos | cos | = a | |||||||||||||||||||||
| 2 | 2 | 2 |
|
| α + γ | ||||||||||||||||
cos | = cos | = cos | ||||||||||||||||
| 2 | 2 | 2 |
|
| |||||||||||||||
cos | = cos | = | ||||||||||||||
| 2 | 2 |
| −(β + γ) | β + γ | |||
= cos | = cos | . | ||
| 2 | 2 |
| α + β | α + γ | β + γ | ||||
Ostatecznie a = 4cos | cos | cos | . | |||
| 2 | 2 | 2 |
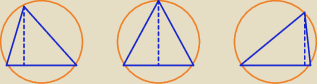 Wracam do zadania b.:
Wśród wszystkich trójkątów (niekoniecznie równoramiennych) wpisanych w koło o promieniu R
znaleźć ten, który ma największe pole.
Proponuję takie rozwiązanie:
Wybieramy dowolny bok trójkąta wpisanego w koło o promieniu R i zadajemy sobie pytanie:
która z wysokości trójkąta poprowadzona do tego boku jest najdłuższa? (bo najdłuższa
wysokość zapewnia największe pole trójkąta).
Stwierdzamy, że najdłuższa wysokość leży na symetralnej wybranego boku, a trójkąt jest
trójkątem równoramiennym, a który z trójkątów równoramiennych ma największe pole − zostało
pokazane wyżej.
Proponuję inne jeszcze podejście do tego zagadnienia.
Przeprowadźmy następujące rozumowanie:
W trójkącie wpisanym w koło o promieniu R najdłuższa wysokość leży na symetralnej
wybranego boku, a trójkąt jest trójkątem równoramiennym.
Stwierdzenie to jest prawdziwe dla wszystkich wysokości tego trójkąta, a więc trójkąt jest
trójkątem równobocznym.
Czy to rozumowanie jest poprawne?, proszę o wypowiedzi.
Wracam do zadania b.:
Wśród wszystkich trójkątów (niekoniecznie równoramiennych) wpisanych w koło o promieniu R
znaleźć ten, który ma największe pole.
Proponuję takie rozwiązanie:
Wybieramy dowolny bok trójkąta wpisanego w koło o promieniu R i zadajemy sobie pytanie:
która z wysokości trójkąta poprowadzona do tego boku jest najdłuższa? (bo najdłuższa
wysokość zapewnia największe pole trójkąta).
Stwierdzamy, że najdłuższa wysokość leży na symetralnej wybranego boku, a trójkąt jest
trójkątem równoramiennym, a który z trójkątów równoramiennych ma największe pole − zostało
pokazane wyżej.
Proponuję inne jeszcze podejście do tego zagadnienia.
Przeprowadźmy następujące rozumowanie:
W trójkącie wpisanym w koło o promieniu R najdłuższa wysokość leży na symetralnej
wybranego boku, a trójkąt jest trójkątem równoramiennym.
Stwierdzenie to jest prawdziwe dla wszystkich wysokości tego trójkąta, a więc trójkąt jest
trójkątem równobocznym.
Czy to rozumowanie jest poprawne?, proszę o wypowiedzi.


 (zadając pytanie, miałem na myśli rozwiązanie takie jak pierwsze)
a jeśli chodzi o zadanie Godzia, to można też je rozwiązać (wiem, że to trochę poza programem
szkolnym, ale Godzio chyba się interesuje takimi rzeczami) używając liczb zespolonych.
Rachunek może nie będzie krótszy niż te sprytne podane wyżej, ale nie wymaga żadnej
pomysłowości
(zadając pytanie, miałem na myśli rozwiązanie takie jak pierwsze)
a jeśli chodzi o zadanie Godzia, to można też je rozwiązać (wiem, że to trochę poza programem
szkolnym, ale Godzio chyba się interesuje takimi rzeczami) używając liczb zespolonych.
Rachunek może nie będzie krótszy niż te sprytne podane wyżej, ale nie wymaga żadnej
pomysłowości 
| eix + e−ix | ||
w zasadzie wystarczy w tym celu znać wzór cos x = | i przekształcać | |
| 2 |
| α+β | γ+α | |||
4 cos | cosU{β+γ}2 cos | = ... (skoncze pozniej, musze isc  ) ) | ||
| 2 | 2 |
| 1 | ||
... = | (ei(α+β)/2 + e−i(α+β)/2) (ei(β+γ)/2 + e−i(β+γ)/2) (ei(γ+α)/2 + | |
| 2 |
| 1 | ||
= | (eiα + e−iα + (podobne wyrażenia z β i γ) + eiπ/2 + e−iπ/2 ) | |
| 2 |

 ale dopiero jak zacznę przerabiać
liczby zespolone
ale dopiero jak zacznę przerabiać
liczby zespolone 