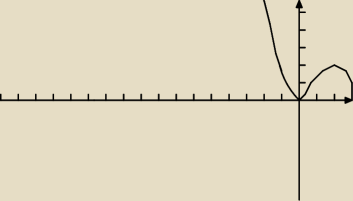
Funkcja Godzio: Proszę o sprawdzenie i ewentualne poprawienie Przebieg zmienności funkcji

	1
f(x) =		x2 * √5 − 2x
	2

D: x ∊(−∞,2,5> ZW: (0,∞) Miejsca zerowe: x = 0, x = 2,5 f(0) = 0 Granice:

	1		x2*√5−2x
limx−>−∞ =		x2 * √5−2x = limx−>∞		=
	2		2(5−2x)

	x2		√5−2x
limx−>−∞		*		= ∞
	x		10   − 2 x

	1
limx−>2,5 =		x2 * √5−2x = 0
	2

Pierwsza pochodna

	1		1
f'(x) = (		x2)'√5−2x = (		x2)'*√5−2x + x2*(√5−2x)'=
	2		2

1		1
	* 2x * √5−2x + x2 *		* (−2) =
2		2√5−2x

	x2
x√5−2x −
	√5−2x

Czy coś jeszcze trzeba liczyć ?

b.: wyglada ok mysle, ze dobrze byloby jeszcze znalezc przedzialy monotonicznosci (zbadac znak f')

Godzio: No i tutaj nie wychodzi f'(x) > 0

	x2
x√5−2x −		> 0
	√5−2x

x(5−2x) − x² > 0 x(−3x + 5) > 0

	5
x∊(0,		)
	3

Godzio: bo to chyba powinno być (0,2)

b.: aha zgubiles czynnik 1/2 w liczeniu pochodnej: masz: + x²*(√5−2x)'

	x2
a powinno byc: +		*(√5−2x)'
	2

b.: oczywiscie zle napisalem pierwiastek: √5−2x, a nie √5−2x

Godzio: ano tak Dzięki