Równanie Godzio: Poproszę o sprawdzenie W przedziale [0,2π] rozwiązać równanie: 1 − tg²x + tg⁴x − tg⁶x + ... = sin²3x

1
	= sin23x
1+tg2x

1
	= sin23x
cos2x + sin2x   cos2x

cos²x = sin²3x cos²x − sin²3x = 0 (cosx − sin3x)(cosx + sin3x) = 0

	π
cosx = cos(		− 3x)
	2

	π		π
x =		− 3x + 2kπ v x = −		+ 3x + 2kπ
	2		2

	π		π
4x =		+ 2kπ v −2x = −		+ 2kπ
	2		2

	π		1		π
x =		+		kπ v x =		+ kπ
	8		2		4

cosx = sin(−3x)

	π
cosx = cosx(		+ 3x)
	2

	π		π
x =		+ 3x + 2kπ v x = −		− 3x + 2kπ
	2		2

	π		π
−2x =		+ 2kπ v 4x = −		+ 2kπ
	2		2

	π		π		1
x = −		+ kπ v x = −		+		kπ
	4		8		2

	5π
i dlaczego jedną z odpowiedzi nie jest:		?
	8

jest jeszcze ich kilka ale już nie pisałem

	π		7π		9π		15π
wg. odpowiedzi to tylko:
	8		8		8		8

Godzio: oczywiście jeszcze założenie

	π
x ≠		+ kπ
	2

Lucyna: Godzio a jakie znaczenie ma fakt że 3x równie dobrze może być kątem z I ćwiartki jak i z 3 ćwiartki

Lucyna: lub 2... na razie taka jedna rzecz mi się rzuciła w oczy.

kanikuła: warunek: ciąg jest zbieżny dla IqI <1

Jack: uwzględniłeś założenie że |tg²x|<1?

Lucyna: kanikuła ale zauważ że mamy do czynienia z szeregiem nieskończonym....

Godzio: a no tak zapomniałem kompletnie o tym warunku Dzięki, tego mi brakowało Nie wiem o co Ci chodzi Lucyna

Lucyna: ups ok sama zauważam cofam sorki mea culpa ma być ten modół

Lucyna: dobra, zaczynam bredzić to znaczy że pora iść spać miłego wieczoru zostającym

kanikuła: I o to "biega"

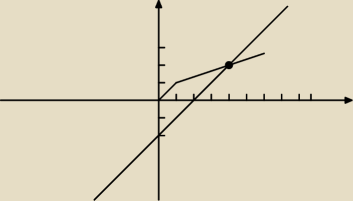
Godzio: Wyznacz dziedzinę i zbiór wartości funkcji f(x) = √2 + √x − x x ≥ 0 √x ≥ x − 2 Można to zrobić w sposób graficzny ? x ∊ <0,4> skoro mam już to to przydało by się zbiór wartości a co za tym idzie pochodna i z tego co ja naliczyłem to ciągle mi wychodzi jakaś głupota może ktoś mi napisać jak trzeba by było pochodną z tego obliczyć?

Godzio: Ja to tak próbowałem robić:

	1		1
f'(x) = (√2 + √x − x)' =		* (		− 1)
	2√2+√x−x		2√x