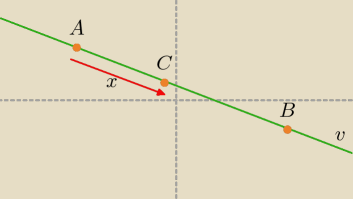
współrzędne punktu na prostej względem odległości od punktu innego Aser: Treść: Wzór obliczający współrzędne punktu C na prostej v właściwości punktu C: − znajduje się pomiędzy punktami A i B, − odległy od punktu A o wartość x

Aser: zapomniałem dodać, znane są tylko wartości punktu A, B, oraz odległość x

Jack: C= A(1−x) + xB − A,B,C rozumiem jako wektory ze współrzędnymi punktów.

Aser: dobra teraz ide poszukać mnożenie i dodawanie wektorów PS: masz Ci los, za szybko odpowiedziałeś i jestem w szoku

Jack: po prostu bierzesz współrzędną "x" każdego z punktów i masz równanie. Podobnie równanie układasz dla współrzędnej "y".

Aser: chwilka powoli, mam rozumieć, że tak? Cx = Ax(1−X)+XBx Cy = Ay(1−X)+XBy ?

Jack: właśnie tak.

Aser: dziękuję bardzo, idę wypróbować

Jack: Testuj ... ale tylko na prostych między punktami A i B.

Aser: zajefajnie wreszcie mogę się poruszać po scenie ^^ (opengl) tryb FPP taki miałem pomysł żeby w ten sposób to zrobić ale nie wiedziałem od której strony się za to wziąść więc musiałbym odkrywać ameryke na nowo możesz mi jeszcze pokrótce wyjaśnić w jaki sposób to działa ta funkcja? nie chcę tego zapamiętywać czy kopiować tylko zrozumieć najlepiej

Aser: o mam jeszcze 1 z dwóch małych problemów teraz wiem jak przesunąć punkt A w miejsce C o długość x potrzebuje przesunąć punkt B o tą samą długość x i ten sam kierunek jeśli możesz a później w nowym temacie podam następny problem

Jack: ważne, żeby suma współczynników była równa 1 oraz x∊[0,1]. Wtedy nie wyskoczysz poza punkty A i B. Skąd się to bierze? Hmm pamiętam że kiedyś na algebrze liniowej gość dokładnie wyprowadzał skądś−tam... Teraz rozumiem to raczej intuicyjnie, że tak musi być.

Jack: nie rozumiem dobrze.... Chcesz przesunąć punkt B wzdłuż prostej v o długość x w kierunku jak pokazuje strzałka na rysunku?

Aser: dokładnie

Jack: Trzeba na początek znać wektor po prostej. Policzymy go w=[Bx−Ax,By−Ay]=[Δx, Δy]. Teraz ustalimy mu długość x. W tym celu wymnożymy go przez pewną liczbę a. x=a√Δx²+Δy²

	√Δx2+Δy2
a=
	x

Szukana liczba "a" jest dana takim wzorem jak wyżej. Jak wymnożysz wektor przez nią, otrzymasz wektor porządnanej długości.

Jack: teraz przykładasz do punktu B wektor w' (ten wymnożony przez a). D=B+w' gdzie D to punkt na którym zatrzyma się wektor w'. Jeśli weźmiesz przeciwny wyraz a, czyli −a przeleciesz w przeciwną stronę (czyli przeciwnie do strzałki).

Aser: co podać za 'a' (wektor czy wartość i ile)?

Aser: rozdzielmy to na parę części: B = w' * a a? Dx = Bx + Wx Dy = By + Wy ?

Jack: wiesz co, odwrotnie przekształciłem wzór na "a"

	x
powinno być a=
	√Δx2+Δy2

"a" powinno wyjść w rachunkach. Twoje dane to A,B oraz x. W tego wyliczysz "a". "a" to liczba przez którą będziesz mnożył wektor w, żeby nadać mu odpowiednią długość.

Aser: o teraz do mnie dociera

Jack: A, B, x −dane w=[Bx−Ax,By−Ay]=[Δx, Δy]

	x
w'=w*a , a=
	√Δx2+Δy2

Dx=Bx+w_x' Dy=By+w_y'

Jack:

Aser: już się martwiłem że nie zobaczę rozwiązania (net robi fikusy) ide to zaaplikować i powiem co się dzieje

Jack:

Aser: Wx' = Wx * a Wy' = Wy * a ?

Jack: tak

Aser: i wszystko zaczęło się sypać ^^ trochę posiedzę nad tym zanim funkcje będą ze sobą współpracować, ale trzeba się z tym przespać dzięki za wszystko, a w miedzy czasie napisze nowy temat z kolejnym problemem i idę spać rano zobaczę odpowiedź

Jack: co się sypie? Możesz wskazać wynik? Próbuj wprowadzić jakies proste dane i na boku sobie policzyć. Ja u siebie na tablicy dostałem to, co miało wyjsc...

Aser: chodzi oto, ze muszę to przełożyć na język Pythona i w odpowiednich miejscach, gdyż punkt A to miejsce gdzie znajduje się kamera punkt B to miejsce gdzie patrzy kamera i te właśnie punkty przesuwam gdy poruszam strzałkami do przodu i do tylu natomiast myszka obracam punkt B wokol punktu A na promieniu r

Jack: wow Przyczyniam się do czegoś wielkiego widzę Powodzenia!

Aser: i kapa gdzies jest błąd, bo nie moge juz poruszać punktem B wokół punktu A kod programu, znajdziesz się w nim # stopnie na radiany rot_zr = (math.pi * rP.tVec[1] ) /180 rot_xy = ( math.pi * rP.tVec[0] ) / 180 # rP.tVec[0] # wzpolrzedne punktu na osi "promień".Y Dz = r_static * math.cos( rot_zr ) r = r_static * math.sin( rot_zr ) Bx = r * math.cos( rot_xy ) By = r * math.sin( rot_xy ) if ( move_fb_old != move_fb ): x = move_fb − move_fb_old Cx = Ax * ( 1 − x ) + x * Bx Cy = Ay * ( 1 − x ) + x * By delta_x = Bx − Ax delta_y = By − Ay # jesli wynik 0 to skalar = 1 if math.sqrt( ( delta_x * delta_x ) + ( delta_y * delta_y ) ) == 0: skalar = 1 else: skalar = x / math.sqrt( ( delta_x * delta_x ) + ( delta_y * delta_y ) ) skalar_prim_x = delta_x * skalar skalar_prim_y = delta_y * skalar Dx = Bx + skalar_prim_x Dy = By + skalar_prim_y

Ada: Kamień spada swobodnie z wysokości 3 metrów. Oblicz czas ruchu kamienia. Przyśpieszenie ziemskie g=9,81ms2

Aser: ? Ada nie tu

Ada: a gdzie?

Aser: Ada: to inne temat, załóż własny Jacek: nie oblicza Dxy

Ada: zakładałam pomóżcie mi proszę

Jack: sprawdź co wylicza w Bx / By i skalar_prim_x/skalar_prim_y

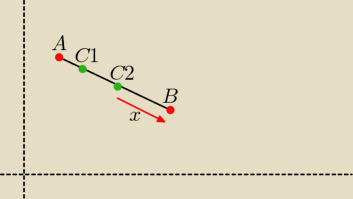
lukas: Witam. Szukam w internecie po omacku rozwiązania problemu i wydaje mi się, że ten temat jest jego rozwiązaniem, ale albo czegoś nie rozumiem, albo coś źle liczę, albo ten sposób jest nieodpowiedni. Rzeczywiste dane odcinka z AutoCAD'a: długość powyższego odcinka: 44.7214 mm A=(X10,Y40) B=(X50,Y20) x=20 C2=(X32.1115,Y28.9443) Potrzebuje wzór jakim posługują się programiści AutoCAD do skracania odcinków o podaną wartość x. Pozdrawiam i z góry dziękują za pomoc

lukas: Już sobie poradziłem Tradycyjnie jak człowiek się poradzi, to zaraz znajduje rozwiązanie.

	nx1 + mx2		ny1 + my2
Skorzystałem ze wzoru: m=		,
	m+n		m+n

1. Znając współrzędne odcinka AB, trzeba policzyć długość odcinka. 2. za m podstawiamy wartość, o którą chcemy skrócić odcinek 3. za n podstawiamy długość odcinka − m 4. zamiast m+n można od razu wpisać długość odcinka. Żeby było zabawnie, to tak jak Aser, potrzebowałem tego do napisania programu komputerowego