Rozwiaz nierownosci Mati: Nierownosci. a. −3(x−2)(x+4) > 0

	1
b.		(x+1) (x−1) ≥ 0
	2

c. −5 (x−√2) (x=3√2) ≥ 0 d. 2(x−7) x < 0 e. −x(2x − 5) ≤0 f. 3(x+6)² ≤ 0 g. x(1−3x) < 0 h. 4x² ≤ 5x i. x > 6x² j. (−x+5)(x+2) > 0 k. (1+x)(3−2x) ≤ 0 l. √3x² + 3x < 0 m. x² < 2 −x

	1
n. 3x2 + 1 > 2		x
	2

o. x−7 ≥ 5x²

	1
p.		x2 − x ≥ 1
	2

r. 4x² + 49 ≤ 28x s. 3x² + 7 ≥ 5x Bardzo prosze o rozwiazanie , od tego zadania zalezy czy zdam

Mati: bardzo prosze o pomoc

Godzio: mogę Ci pomóc rozwiązać 4 nierówności i je wytłumaczyć tak żebyś z resztą sobie poradził chcesz ?

Godzio: Bo wątpię żeby komukolwiek chciało się tyle przykładów rozwiązywać a jeśli chcesz zdać to też trzeba się czymś wykazać

Mati: no pewnie

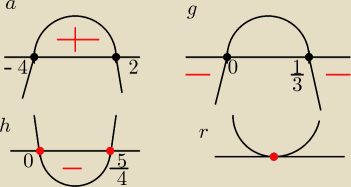
Godzio: Niech już będzie 5 przykładów a) , g) , h) , r) l) − nie miało być przypadkiem √3x² ? a) − 3(x−2)(x+4) > 0 szukasz miejsc zerowych tzn, dla jakich x wyrażenie będzie równe zero: x − 2 = 0 => x = 2 x + 4 = 0 => x= −4 Miejscami zerowymi tej funkcji są 2 i −4, które zaznaczasz na osi i rysujesz parabolę mamy −3(x−2)(x+4) więc ramiona będą do dołu i sprawdzasz gdzie wartości są dodatnie W tym wypadku mamy: x ∊ (−4,2) g) x(1−3x) < 0 tak samo jak w poprzednim wyznaczamy miejsca zerowe

	1
x = 0 v x =		, rysujemy parabolę i sprawdzamy gdzie przyjmuje wartości ujemne
	3

parabola z ramionami do dołu bo po wymnożeniu przy najwyższej potędze jest " − " x(1−3x) = −3x² + x

	1
Odp: x ∊(−∞,0)∪(		,∞)
	3

h) 4x² ≤ 5x − przenosimy wszystko na jedną stronę i wyciągamy x przed nawias 4x² − 5x ≤ 0 x(4x − 5) ≤ 0

	5
miejsca zerowe: x = 0 v x =		− parabola z ramionami do góry
	4

	5
Odp: x ∊ <0,		>
	4

r) 4x² + 49 ≤ 28x 4x² − 28x + 49 ≤ 0 tutaj żeby wyznaczyć miejsca zerowe trzeba policzyć deltę a = 4 b = −28 c = 49 Δ = b² − 4ac = 28² − 16 * 49 = 0 (możesz zapamiętać jeśli Δ=0 to zawsze funkcja kwadratowa jest wzorem skróconego mnożenia w tym wypadku (2x − 7)² ) jeśli Δ = 0

	−b		28		7
to jest jedno rozwiązanie: xo =		=		=
	2a		8		2

Pytanie było dla jakich argumentów funkcja przyjmuje wartości mniejsze lub równe zero: mniejszych od zera nie przyjmuje a równe zero jest tylko miejsce zerowe

	7
Odp: x ∊ {		}
	2

Mati: dzieki wielkie

Mati: w l mozliwe ze bylo tak jak mowisz

Ewka: −x2+3x ≤ 0 x2−6+9≤0 2x−5x≥0 −x2+4x≤0

Hajtowy: ..... −x(x−4) ≤ 0 x=0 v x=4 Parabolkę i zaznaczać

Ela: bardzo proszę o pomoc rozwiąż nierówność x²−4/x²−5x=0

trututu: ale to jest równanie ela, nie nierówność na moje oko dziedzina: x² −5x≠0 x(x−5)≠0 x≠0 ∨ x≠5 D: x∊ R/ {0,5} x² − 4 =0 x=2 ⋁ x=−2

needhelp: x−7≥5x² Proszę o pomoc w tej nierówności . U

Ola: 2/3x+1≥1/2x−2

ICSP:

2		1
	x + 1 ≥		x − 2 // * 6
3		2

4x + 6 ≥ 3x − 12 x ≥ − 18