Udowodnij, że ... Aniss: Udowodnij, że punkt styczności okręgu wpisanego w trójkąt prostokątny z przeciwprostokątną dzieli tę przeciwprostokątną na odcinki, których iloczyn jest równy polu tego trójkąta.

Godzio:

	ab
P =
	2

	a+b−c
r =
	2

a² + b² = c²

	2a − a − b + c		2b − a − b + c		a − b + c		b − a + c
(a−r) * (b−r) =		*		=		*
	2		2		2		2

ab − a2 + ac − b2 + ab − bc + cb − ca + c2		−a2 + 2ab − b2 + c2
	=		=
4		4

−a2 + 2ab − b2 + a2 + b2		2ab		ab
	=		=
4		4		2

Eta:

	ab
P=
	2

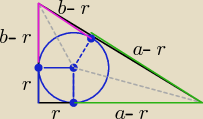
	ab
P= (a−r)*r + (b−r)*r + r2= ar+br− r2 =
	2

wykażemy,że:

	ab
P= ( a−r)(b−r) = ab −ar −br+r2 = ab − (ar+br−r2)= ab − ab2=
	2

c. n. u

Eta: Godzio i jak? ........ krócej ?

Godzio: No tak Rzadko mi się zdarza zrobić najkrócej jak się da przy zadaniach tego typu

Godzio: To tego to jednak trzeba mieć umysł

Eta: Nie bądź taki skromny

Godzio: E tam, teraz koniec szkoły się zbliża to już panuje bardziej atmosfera "rozluźnienia" to i człowiek mniej myśli Tak samo jak dzisiaj zobaczyłem komentarz coś w stylu: "możesz za mnie to obliczyć pod przed wakacjami już mi się nie chce liczyć"

Eta: Czytałam

Godzio: Teraz tak sobie myślę Czy lepiej w ogóle nie spać czy pójść i o 7 nie mieć sił żeby wstać

Eta: Koniecznie do spania Ja mogę posiedzieć, bo śpię do 12⁰⁰ Dobranoc

Godzio: No Dobranoc ale i tak nie jestem śpiący