: Oblicz obwód kwadratu wpisanego w okrąg o promieniu 2π Misiek: : Oblicz obwód kwadratu wpisanego w okrąg o promieniu 2π

klf:

	1
promień okręgu=		przekątnej kwadratu→ 2π=12a√2
	2

klf: 4π=a√2 teraz podziel przez pierwiastek zeby otrzymac dlugosc boku kwadratu ^4π_√2 = a a=^4π√2₂

mila: narysujesz kwadrat w okręgu to zobaczysz,że przekątna kwadratu jest średnicą okręgu czyli promien=1/2*d to d=2r r=2π d=2*2π=4π bok kwadratu a z Pitagorasa a²+a²=d² 2a²=(4π)² 2a²=16π²/:2 a²=8π² /√ a=√8π obw=4a=4√8π

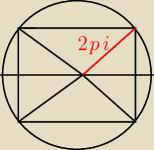
Wojciech: czyli możemy sobie ten kwadrat podzielic na 4 trojkaty o jednkowych polach. A wiec wystarczy ze wyliczymy 1 i pomnozymy razy 4. No wiec z twierdzenia pitagorasa bedzie tak: 2π² + 2π² =c² 8π²=c² c=√8π² c=2√2π 2√2π *4 = 8√2π Pole = 8√2*3,14 ≈ 35,5