pomocy mateusz: dla jakich wartości parametru m rownanie |x²−4|=m²+1 ma dwa rozne rozwiazania wiec narysowalem wykres |x²−4| ale nie wiem co dalej. czy ktos wytlumaczy.. ogolnie co robi sie w tego typu zadaniach.

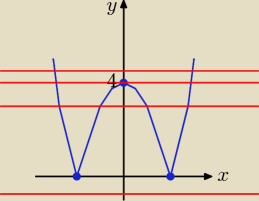
Bogdan: Podaję wskazówki. Mamy tu dwie linie: y = |x² − 4| oraz y = m² + 1 (ta linia jest linią prostą równoległą do osi x) Brak rozwiązań (linie nie mają punktów wspólnych) dla m² + 1 < 0 Są 2 rozwiązania (linie mają 2 punkty wspólne) dla m² + 1 = 0 lub dla m² + 1 > 4 Są 3 rozwiązania (linie maja 3 punkty wspólne) dla m² + 1 = 4 Są 4 rozwiązania (linie mają 4 punkty wspólne) dla 0 < m² + 1 < 4

mateusz: rzeczywiscie.. robilem tak ale cos mi zle wyszlo i stwierzilem ze w przyadku kwadratu przy m robi sie to inaczej.. a jednak bardzo podobnie dziekuje,

Bogdan: Robi się tak samo, bez względu na to, jakie wyrażenie zawarte jest we wzorze linii prostej. Analiza wzoru prostej z parametrem m lub innym określa szczegóły rozwiązania. W tym przypadku równość m² + 1 = 0 dla m∊R oczywiście nie zachodzi.