Zadanie Godzio: Mam takie zadanko z matury (1975 r. ) i jestem ciekaw czy dobrze rozwiązałem Napisz równanie stycznej i normalnej (tj. prostopadłej do stycznej w punkcie styczności) do paraboli y² = 2x w punkcie mającym rzędną 2. Oblicz pole figury zawartej między łukiem paraboli dla y ≥ 0 wyznaczoną normalną i osią OX y = ax + b y² = 2x 2 = ax + b 4 = 2x => x = 2 2 = 2a + b b = 2 − 2a y = ax + 2 − 2a (ax + 2 − 2a)² = 2x a²x² + 4ax + 4 − 4a²x − 8a + 4a² = 2x a²x² + x(4a − 4a² − 2) + 4a² − 8a + 4 = 0 Δ = 16a² + 16a⁴ + 4 − 32a³ − 16a + 16a² − 4a²(4a² − 8a + 4) = 16a⁴ − 32a³ + 32a² − 16a + 4 − 16a⁴ + 32a³ − 16a² = 16a² − 16a + 4 = 0 4a² − 4a + 1 = 0 (2a − 1)² = 0

	1
a =
	2

	1
y =		x + 1 − styczna
	2

prostopadła: 2 = −2 * 2 + b b = 6 y = −2x + 6 To jest dobrze rozwiązane ? Pola liczyć jeszcze nie umiem także to tylko chodzi mi o tą część zadania.

Basia: dobrze, a chcesz wiedzieć jak to rozwiązanie powinno wyglądać w 1975 roku ?

Godzio: oczywiście

Basia: dodam, że zajmuje jakieś pięć krótkich linijek tekstu

Godzio: pewnie coś z pochodnymi tak mi się wydaje

Basia: y² = 2x y = √2x lub y=−√2x interesuje nas rzędna =2 czyli f(x)=√2x

	1		1
f'(x) =		*2 =
	2√2x		√2x

√2x=2 2x=4 x=2 A(2,2)

	1		1
a = f'(2)=		=
	√2*2		2

y=ax+b y=¹₂x+b 2=¹₂*2+b b=1 styczna: y=¹₂x+1 normalna oczywiście już tak jak liczyłeś P=∫₀²√2xdx +∫₂³(−2x+6)dx to też maturzysta musiał umieć policzyć ( to na pewno był profil mat−fiz)

Godzio: zgadza się profil mat − fiz na pewno łatwiej i szybciej szkoda że już tego w szkole nie uczą

Godzio: Zaraz dam jeszcze jedno wraz z moim rozwiązaniem ale to już będzie bardziej zagmatwane (oczywiście tym sposobem co ja bd robić )

Godzio: I jeszcze jedno W punktach o odciętych x₁ = 1 x₂ = −1 poprowadzono styczne do wykresu funkcji

	1+3x2
f(x) =		. Znajdź współrzędne punktu przecięcia się tych stycznych.
	3+x2

	1+3x2
f(x) =
	3+x2

x₁ = 1

	1 + 3
y =		= 1
	4

x₂ = −1 y = 1

1 + 3x2		3x2 + 9 − 8		8
	=		= 3 −
3 + x2		3 + x2		3+x2

I teraz pytanie jak w ogóle poprowadzić te styczne skoro ma mieć ona jedynie 1 pkt wspólny ? y = ax + b y = a₁x + b₁ 1 = a + b 1 = −a₁ + b₁ b = 1 − a b₁ = 1 + a₁ y = ax + 1 − a y = a₁x + 1 + a₁

	1+3x2
f(x) =
	3+x2

(ax + 1 − a)(3+x²) = 1 + 3x² 3ax + ax³ + 3 + x² − 3a − ax² = 1 + 3x² ax³ + x²( − 2 − a ) + 3ax − 3a + 2 = 0 W(1) = a − 2 − a + 3a − 3a + 2 = 0 ax² − 2x + 3a − 2 ax³ + x²(−2−a) + 3ax − 3a + 2 : (x − 1) −ax³ + ax² −−−−−−−−−−−−−−− −2x² + 3ax − 3a + 2 2x² − 2x −−−−−−−−−−−−−−− x(3a − 2) − 3a + 2 −x(3a − 2) + 3a − 2 −−−−−−−−−−−−−−−−−−−−−−−−−−−− = = (x−1)(ax² − 2x + 3a − 2) = 0 Δ = 4 − 4a(3a − 2) = 4 − 12a² + 8a = −12a² + 8a + 4 = 0 −3a² + 2a + 1 = 0 Δ = 4 + 12 = 16

	−2 + 4		1
a1 =		= −
	−6		3

	−2 − 4
a2 =		= 1
	−6

y = ax + 1 − a

	1		4
y = −		x +
	3		3

y = x i tutaj się zatrzymam bo nie wiem czy jest sens dalej liczyć. I gdybyś Basiu mogła zrobić takie normalne rozwiązanie to bym był bardzo wdzięczny bo planuje w niedługim czasie przerobić sobie pochodne, granice, całki

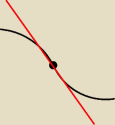
Basia: mniej więcej tak wiem, że to dziwnie jak na styczną wygląda, ale jednak jest to styczna mój rysunek jest bardzo niedoskonały, ale może coś z niego zrozumiesz poza tym napiszę za chwilę wzory tych stycznych i spróbujesz to sobie narysować na kartce, powinieneś się połapać "o co biega" podobnie wygląda styczna do wykresu f(x)=x³ w punkcie x₀=0

Godzio: ok a rysunek rozumiem, dziwnie to wygląda dlatego że styczna zazwyczaj ociera się o funkcję a tutaj po prostu przez nią przechodzi

Basia: wszystko co policzyłeś jest poprawne, a jednak ⁻¹₃ nie jest współczynnikiem kierunkowym stycznej; jest nim tylko 1 a jest tak dlatego, że nie każda prosta, która ma z wykresem funkcji jeden punkt wspólny jest styczną do tego wykresu jest tak w przypadku funkcji kwadratowych, ale innych już nie przykład chyba oczywisty to: f(x)=x³ i prosta y=1 albo f(x)=logx i prosta y=−x+4

Godzio: czyli styczna to taka prosta mająca jeden punkt wspólny i ocierająca się o jego "fale" tak jak w tym przypadku ?

Godzio: Dobra to w takim razie wiedząc to to już bym sobie poradził z rozwiązaniem Dzięki wielkie Basiu

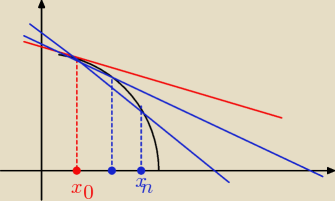
Basia: styczna (czerwona) do krzywej w punkcie x₀ to granica do której dążą sieczne (niebieskie) przechodzące przez punkty A(x₀, f(x₀)) i B_n(x_n, f(x_n)) gdy x_n → x₀ współczynniki kierunkowe tych siecznych to

	f(x0)−f(xn)
an =
	x0−xn

współczynnik kierunkowy siecznej musi więc być granicą tych a_n przy x_n→x₀ stąd:

	f(x0)−f(xn)
a = limxn→x0		= f'(x0)
	x0−xn

ściślej:

	f(x0)−f(x0+h)
a = limh→0		= f'(x0)
	h

często jest też stosowany zapis

	f(x0)−f(x0+δx)
a = limδx→0		= f'(x0)
	δx

gdzie δx oznacza przyrost argumentu x

Basia: trwało to chwilę, moje zdolności rysunkowe są mniej niż średnie (łagodnie mówiąc)

Basia: pisać rozwiązanie z pochodną ?

Godzio: a długo to zajmie? bo nie chce Cię "nadwyrężać"

Basia: obrazowo, jest właśnie tak jak napisałeś

Basia: nie tak bardzo długo, tym bardziej, że tego co już policzyłeś nie będę powielać

Basia: A(1,1) B(−1,1)

	6x(3+x2)−2x(1+3x2)
f'(x) =		=
	(3+x2)2

18x+6x3−2x−6x3
	=
(3+x2)2

16x
(3+x2)2

	16
f'(1)=		=1
	16

	−16
f'(−1)=		=−1
	16

y=x+b 1=1+b b=0 styczna w punkcie A: y=x y=−x+b 1=−(−1)+b b=0 styczna w punkcie B: y=−x resztę sam policzysz

R.W.16l: Jezu, jak patrzę na te wasze wywody, to omniemuję (jeśli takie słowo istnieje)

Basia: nie ma; oniemiejesz nie taki diabeł straszny, tylko tutaj to nie jest "od początku"

Jack: swoją drogą pojęcia nie mam, czemu pochodnych i granic ma nie być już na maturze... To jest prostsze niż np. wyprowadzanie wzoru na pole trojkąta z tw. sinusów

Eta: Hehe ....... skąd ja to znam To była pierwsza matura ......... (za czasów mojej pierwszej pracy w szk. średniej

;p: a co jacek wytlumaczys zmi calki i pochodne?

Jack: pewnie, zapraszam na korepetycje (chodziło mi szczególnie o szerokie zastosowania, ilustrację i prostotę rozwiązywania niektróych zadań)

;p: hehe mozna tutaj?

Kejt: dobre pytanie

;p: jakie studia polecacie?

Jack: hehe to wymaga troszkę przygotowania, a potem czasu żeby odpowiednio to przedstawić (słowo pisane jest trudniej przyswajalne niż mówione) . Znacznie prościej w 4 oczy Czasem pojawiają się na forum przykłady z całek czy pochodnych − można na ich przykładzie się poduczyć.

;p: ok sprobuje

Jack: zależy co Cię interesuje

;p: wlasnie nie wiem

Jack: to idź na filozofię − czegoś sie dowiesz o sobie

;p: hehhe odpada

Eta: Hehe ...... pewnikiem ..."cał(k)owanie" Jack

;p: cos scislego tylko co teraz najlepiej wybrac

;p: ktos moze jest z politechniki.rzeszowskiej?

;p: Eta Jack a wy na czym jestescie?

Jack: Ja na matematyce.

;p: i jak?a co miales z matmy w Lo a i jeszcze na politechnice?

Basia: Eta i ja też, tyle, że "po".

;p: a ok a mozna wiedziec gdzie? i pewnie uczycie teraz w szkole tak?

Jack: nie, jestem na uniwerku. Z matmy w liceum niewiele pamiętam, bo 1) zdawałem historię i to mnie interesowało, 2) nie są to moje pierwsze studia. Ale pochodne wielomianów na pewno miałem

Basia: Eta uczyła. Teraz już jest na emeryturze. Mnie interesowały raczej "pozaszkolne" dziedziny matematyki. A teraz jestem na urlopie zdrowotnym przed emeryturą.

Eta:

Kejt: hmm.. dziwnie się teraz czuję..

Basia: No co Ty, my jesteśmy młode duchem.

Eta: Jak "dziwnie" Kejt

Kejt: rozumiem, ale zostałam chyba najmłodszą osobą rozwiązującą tutaj zadania. heh..

Eta: Metryka nie jest ważna ...... w "młodym" ciele... młody duch

Kejt: no wiem, wiem. ale mimo to dziwnie..

Eta: My tak z tęsknoty, za tym co minęło i nie wróci .... ( a żaaaaaaal )

Basia: Pociecha dla Kejt ! Godzio jest chyba młodszy. 2 klasa średniej.

Kejt: nie. ja jestem z pierwszej.. nie udało się.

Eta: Kejt ....... moje gratulacje

Kejt: ojej. za cóż?

Basia: Szkoda, że Tim nie bywa już na forum. Byłby młodszy. Kejt powinnaś być z siebie dumna

Kejt: wciąż nie rozumiem dlaczego..

Godzio: Za umiejętności dzięki Basia za tamto musiałem już uciekać

Kejt: ekhm. dziękuję. ale ja nie widzę w tym nic niezwykłego..

Basia:

;p: wlsanie gdzie tIM?!