matma kinguś: nierówności rozwiąż nierówność pomocy w tych zadaniach ,bardzo proszę.pleasee (x−1)(x−2)(x−3)≤0 (1−2x)(x−3)(3x−5)≤0 (1−3x)(x+1)(−3x−3)≥0 (x+1)(2x−3)(x+3)≤0

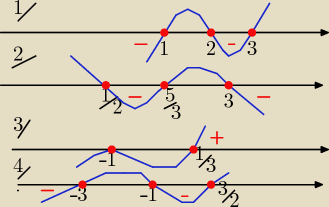
Eta: Masz gotowy rozkład na czynniki ( odczytujesz miejsca zerowe) 1/ x= 1 v x= 2 v x= 3 rysujemy "falę " przez te miejsca , zaczynając rys. od prawej strony od góry bo współczynnik przy x³ jest dodatni wybieramy wartości z pod osi OX wraz z punktami na osi OX ( bo nierówność ≤0 odp: x€ ( −∞, 1> U < 2, 3> 2/ podobnie: x= ¹₂ v x= ⁵₃ v x= 3 tym razem rys. od prawej , ale od dołu ( bo wsp. przy x³ jest ujemny) odp; x€< ¹₂, ⁵₃> U < 3, ∞) 3/ x= −1 −−− pierwiastek dwukrotny v x= ¹₃ rys. od góry i odbija w punkcie x= −1 odp: x€< ¹₃, ∞) U {−1} 4/ podaj podobnie rozwiązanie w 4/

R.W.16l: (x−1)=a (x−2)(x−3)=b ab≤0 gdy a≥0 i b<0 lub a≤0 i b>0 lub a<0 i b≥0 lub a>0 i b≤0 trochę tego jest, ale no coż, trzeba popodstawiać i już i analogicznie resztę! powodzenia

R.W.16l: A można po mojemu

robinka: a dlaczego nie spróbujesz sama, tego zrobić ?

robinka: nie spotkałam się z taką, wydaje mi się, za bardzo zagmatwana

Basia: To p czym pisze R.W.16l to klasyczna metoda algebraiczna na rozwiązywanie nierówności, oparta na rachunku zdań. Dużo pisania, ale z formalnego punktu widzenia właściwie jedyna poprawna. Dla dwóch czynników oczywista: a*b≤0 ⇔ (a≤0 ∧ b≥0)∨(a≥0 ∧b≤0) Dla trzech już jest to znacznie bardziej rozbudowana alternatywa a*b*c≤0 ⇔ (a≤0 ∧ b≤0 ∧ c≤0)∨(a≤0 ∧ b≥0 ∧ c≥)∨(a≥0 ∧ b≤0 ∧ c≥0)∨(a≥0 ∧ b≥0 ∧ c≤0) a dla czterech to już spory koszmar, ale oczywiście da się policzyć.

robinka: dziękuje Basiu za wyjaśnienie

b.: w sposobie R.W.16l lepiej jest chyba rozwiazywac przeciwna nierownosc, bo latwiej jest, gdy nierownosc jest ostra: ab>0 <=> (a>0 i b>0) lub (a<0 i b<0) (tylko 2 koniunkcje, zamiast czterech) oczywiscie wtedy na koniec nalezy wziac dopelnienie zbioru, ktory wyjdzie no ale rysunkowo jest chyba szybciej i latwiej uniknac pomylek

Basia: kwestia przyzwyczajenie; dla dwóch prawie zawsze liczę, bo nie chce mi się rysować dla więcej niż dwóch rysuję, bo nie chce mi się tyle pisać, ale spotkałam się w jakimś zbiorze zadań (nie pamiętam w tej chwili w którym) z wyraźnym poleceniem "rozwiąż algebraicznie nierówności...." na szczęście tylko kwadratowe

mila: Kingus patrzysz na to co jest w nawiasach i myslisz kiedy będzie równe zero x−1=0 x=1 to pierwiastek zaznaczasz go na osi x−2=0 x=2 nastepny pierwiastek zaznaczasz na osi x−3=0 x=3 i teraz ten zaznaczasz na osi To jak narysujesz linie zależy od liczby która stoj przed x o najwyższej potędze. gdybys pomnozyła te nawiasy to najwiekszy byłby x³ nic przed nim nie ma czyli jest1 .1 to liczba dodatnia czyli zaczynasz rysować linie od prawej strony nad osią .Robisz falbankę przechodzac przez zaznaczone pierwiastki rozwiązaniem jest to co na i pod osią bo masz,≤0 w drugim masz 1−2x=0 1=2x /:2 1/2=x to pierwszy pierwiastek zaznaczasz na osi x−3=0 x=3 zaznaczasz 3x−5=0 3x=5 /3 x=5/3 tym razem −2x*x*3x=−6x³ −6 to liczba ujemna dlatego zaczynasz rysowac falbankę od prawej strony pod osią Jeżeli sa dwa takie same pierwiastki ( w zad 3 x=−1) to wtedy falbanka nie przechodzi na drugą sronę osi tylko się od niej odbija

R.W.16l: Ok