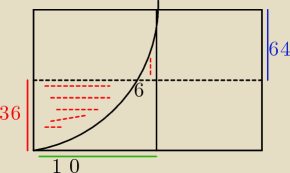
Zadanie Godzio: Basia ratuj ! to jest ramie paraboli y = x² − 36 i musze obliczyc pole tych 2 kawalkow co zamalowalem

Godzio: ta przerywana linia to OX

Basia: Cześć Godzio ! P₁ = − ∫₀⁶(x²−36)dx P₂ = ∫₆¹⁰(x²−36)dx ∫(x²−36)dx = ¹₃x³−36x +C P₁ = − (¹₃x³−36x) |₀⁶= −[ (¹₃6³−36*6)−(¹₃*0³−36*0) ]= − [^6*6*6₃−6*6*6]= 6*6*6 − ^6*6*6₃ = ^{3*6*6*6−6*6*6}₃ = ^2*6*6*6₃=2*2*6*6=4*36=144 P₂ = (¹₃x³−36x) |₆¹⁰=

	103		63
[ (		−36*10)−(		−36*6) ]=
	3		3

	103−36*3*10
[		−(3*36−6*36) ]=
	3

10(100−108)
	−(−3*36) ] =
3

−80
	+3*36 =
3

−80+9*36		−80+324		244
	=		=
3		3		3

P=P₁+P₂ żaden inny sposób nie przychodzi mi do głowy

Godzio: dzięki

Basia: Godzio to Twoje zadanko ? Zajmujesz się całkami ? Czy dla kogoś ? Bo szkolny poziom to nie jest. Już dawno nie, niestety.

Godzio: na informatyke było potrzebne (bo teraz mam) i typek powiedzial ze mamy policzyc pole tego jak chcemy

Basia: jak Wam już powie o co mu naprawdę chodziło to napisz, bo jestem ciekawa wie chyba przecież, że nie znacie rachunku różniczkowego i całkowego

Basia: skoro to na informatykę, to sądzę, że chodzi przybliżenie pola sumą pól prostokątów dzielimy przedział na n równych odcinków u Ciebie to będą: 1. ⁶_n 2. ⁴_n 1. budujemy prostokąty "z niedomiarem" ich pola to ⁶_n*f(0*⁶_n) ⁶_n*f(1*⁶_n) ⁶_n*f(2*⁶_n) .................................... ⁶_n*f((n−1)*⁶_n) P_niedomiarem ≈∑_{i=0...(n−1)} ⁶_n*f(i*⁶_n) budujemy prostokąty "z nadmiarem" ich pola to ⁶_n*f(1*⁶_n) ⁶_n*f(2*⁶_n) ⁶_n*f(3*⁶_n) .................................... ⁶_n*f(n*⁶_n) P_nadmiarem ≈∑_i=1...n ⁶_n*f(i*⁶_n) można przyjąć

	Pniedomiarem+Pnadmiarem
P=
	2

( w rzeczywistości to P = granicy tych sum częściowych przy n→+∞, i nawiasem mówiąc to jest definicja całki oznaczonej Riemana) 2. tutaj będzie tak budujemy prostokąty "z niedomiarem" ich pola to ⁴_n*f(6+0*⁴_n) ⁴_n*f(6+1*⁴_n) ⁴_n*f(6+2*⁴_n) .................................... ⁴_n*f(6+(n−1)*⁶_n) P_niedomiarem ≈ | ∑_{i=0...(n−1)} ⁶_n*f(6+i*⁶_n) | budujemy prostokąty "z nadmiarem" ich pola to ⁴_n*f(6+1*⁴_n) ⁴_n*f(6+2*⁴_n) ⁴_n*f(6+3*⁴_n) .................................... ⁴_n*f(6+n*⁴_n) P_nadmiarem ≈ | ∑_i=1...n ⁴_n*f(6+i*⁴_n) to się znakomicie nadaje do pisania programu liczącego pole (całkę oznaczoną)

Godzio: Chodziło o to żeby zrobić to w przybliżeniu określić pole a dokładnie żeby robić takie trapeziki co pół metra, program napisałem także wszystko ok a to co wyżej napisałaś to się przydało do sprawdzenia wyniku Ja skojarzyłem to z całkami więc odrazu napisałem