Liczby zespolone lukasz: Witam , Chcę nauczyć się rozwiązywać zadania z liczbami zespolonymi i natrafiłem na przykład który nie potrafię rozwiązać , pomóżcie Znaleźć w układzie współrzędnych zbiór opisany następującą nierównością: |z−2+3i|<2 Proszę o pomoc

robinka: http://wms.mat.agh.edu.pl/~zrr/zespolone/ http://wms.mat.agh.edu.pl/~zrr/zespolone/zad4rozw.htm

lukasz: heh , właśnie z tego serwisu mam to zadnie ale tam nie ma rozwiązania , tylko gotowy wykres

robinka: ja to tak rozumie: |z| to okrąg o promieniu (0,0) tu jednak mamy inna sytuacje mamy okrąg o środku (2,−3) oraz promieniu 2, ale mamy warunek <2 czyli obszar w środku ma być zamalowany bez obwodu.

b.: albo inaczej, geometrycznie |z−w| to odległość między punktami z i w tutaj mamy |z − (2−3i) | < 2 i stąd rozwiązaniem jest koło bez brzegu

lukasz: b.: Proszę weź rozpisz ten przykład , bo włączyłeś tylko w nawias

Jack: środek okręgu w punkcie w=2−3i i koła bez brzegu o promieniu 2. Dokładnie tak, jak zapisała robinka.

lukasz: hmm .. ja myślę że tutaj trzeba skorzystać z jakiegoś wzoru , nie jestem pewien , bo tam jest jeszcze to "z"

Jack: "z" to taki "x" tylko że na płaszczyźnie zespolonej.

lukasz: kurcze , jakoś ciężko jest mi ten przykład zrozumieć . A gdyby nie było tego "z" w tym przykładzie to efekt rozwiązania był by taki sam

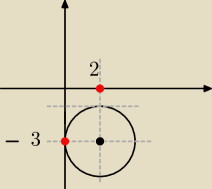
Jack: sprawdź sobie że np. punkt z=−3i daje brzeg koła, tzn. zachodzi równość w powyższej nierówności.

Jack: |z−w|<a , gdzie "a" to promień koła, natomiast "w" można rozumieć jako przesunięcie środka okręgu (względem (0,0) oczywiście).

lukasz: czyli "z" nie odgrywa żadnej roli Musi być z racji że jest to liczba zespolona

Jack: "z" odrywa, to zmienna. To tak jakbyś miał na prostej |x−2|<3 (wiesz że to zbiór punktów odległych od 2 od mniej niż 3). Musi być z racji że mamy liczby zespolone (a więc i płaszczyznę zespoloną).

lukasz: no dokładnie , dzięki wielkie , pomogłeś mi bardzo

Jack: powodzenia dalej

lukasz: dzięki

koza: π≥