Trójkąty podobne. Kris: Dany jest trójkąt ABO, gdzie A(−2,0), B(0,1), O(0,0). Trójkąt prostokątny CDE ma przeciwprostokątną długości √10 i jest podobny do trójkąta ABO. Olicz obwód i pole trójkąta CDE.

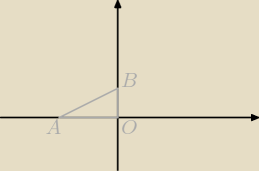
Lucyna: Z rysunku widać gdzie jest przeciwprostokątna, więc liczymy jej długość: |AB| = √(−2−0)² + (0−1)² = √4+1 = √5

	√10
Ponieważ przeciwprostokątna CDE = √10 to skala podobieństwa =		= √2
	√5

tzn, że obwód O_CDE = √2O_ABO P_CDE = (√2)²P_ABO

Kris: Ok, dzięki, tylko, że potrzebuje jeszcze małej podpowiedzi. Bo po tym jak wyliczyłaś k = √2 , to już nie wiem jak mam rozumieć wynik obwodu trójkąta CDE

Lucyna: obwód to suma boków, ponieważ skala to √2 tzn każdy bok trójkąta ABO trzeba przemnożyć przez √2 √2|AO| + √2|OB| + √2|BA| = √2(|AO| +|OB| + |BA|) = √2O_AOB Dlatego w polu trójkąta skala jest do kwadratu, bo tam się mnoży bok razy bok.