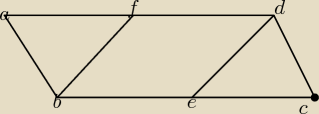
 Równoległobok ABCD ma boki długosci |AB| = P{3} I |AD| = 4 oraz |∡BAD| = 30 stopni. Czworokąt
BEDF jest rombem. Znajdź długość jego boku.
Równoległobok ABCD ma boki długosci |AB| = P{3} I |AD| = 4 oraz |∡BAD| = 30 stopni. Czworokąt
BEDF jest rombem. Znajdź długość jego boku.
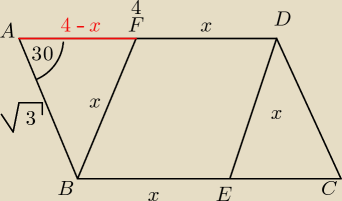 z tw. cos.
x2 = (4−x)2 + √32 − 2 * (4−x) * √3 * cos30
z tw. cos.
x2 = (4−x)2 + √32 − 2 * (4−x) * √3 * cos30
| √3 | ||
x2 = 16 − 8x + x2 + 3 − 2√3 * (4−x) * | ||
| 2 |
| 6 | 1 | |||
x = | = 1 | |||
| 5 | 5 |
| 7 | 2 | |||
x = | = 1 | |||
| 5 | 5 |