zadania xyz: zad.1 w trojkat rownoboczny o boku 8cm wpisano prostokat tak,ze jeden bok zawiera sie w podstawie trojkata, a dwa pozostale wierzcholki prostokata naleza do ramion trojkata. wyznacz dlugosci bokow prostokata, jezeli pola trojkatow przylegajacych do bokow prostokata sa rowne. zad.2 obwod prostokata wynosi 18dm. na bokach prostokata zbudowano polkola o srednicach rownych dlugosciom bokow prostokata. jakie powinny byc wymiary prostokata, aby suma pol czterech polkoli byla najmniejsza? zad.3 pola dwoch trojkatow rownobocznych rozna sie ⁴⁵₄ √3cm², a stosunek dlugosci ich bokow jest rowny 2:3. oblicz dlugosci bokow tych trojkatow.

xyz: ponawiam dziś

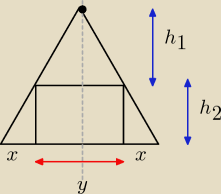
Jack: Rys do 1. Oznaczenie:

	a√3
h=h1+h2 , h − wysokość trójkąta równobocznego h=
	2

a − bok tego trojkąta. a=2x+y

	h1		h
Z tw. Talesa		=		.
	y		a

	h2*x		h1*y		a2√3
Z zadania wiadomo że: 2*		+		+h2=
	2		2		4

	h2*x		h1*y
oraz, że:		=
	2		2

Wystarczy popodstawiać i rozwiązać układ z paroma niewiadomymi.

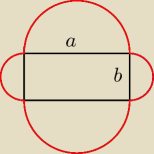
Jack: Widać że te cztery półokręgi tworzą dwa pełne koła: jeden o promieniu a/2, drugi b/2. Z zadania 2a+2b=18 czyli a=9−b Policzymy teraz sumę pół kół P. P=π(^a₂)²+π(^b₂)² Teraz podstawmy a=9−b P=π(^9−b₂)²+π(^b₂)² Teraz zróbmy z tego funkcję zależną od b. P(b)=π(^9−b₂)²+π(^b₂)² Trzeba wyznaczać najmniejszą wartość jaką przyjmuje ta funkcja. Bedzie to pewnie wierzchołek paraboli (współrzędna "x").

Jack: "pewne" bo domyślam się że po uproszczeniu dostaniesz funkcję kwadratową.

Jack: zad 3 napisz wzory na pole trójkąta i... przeanalizuj je.

Kejt: 3.

	a2√3
P=
	4

2x − bok jednego 3x − bok drugiego to będzie coś takiego:

(3x)2√3		45√3		(2x)2√3
	−		=
4		4		4

Jack:

Kejt: ych.. zepsułam. awarię internetu miałam i nie zauważyłam.. wybacz Jack.

Jack: nie ma o czym mówić! Myślę że taka pomoc będzie nawet lepsza, niż moja baaardzo ogólna wskazówka.