pomocy sonia: pomocy! mam narysować obszar całki ∫f(x,y)dydx i jej przedział to od: (2−x) na dole, do (\sqrt{2x−x²}) u góry. i musze to narysować

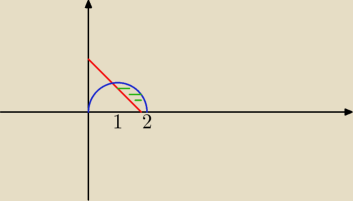
Basia: chodzi tylko o obszar całkowania ? jeżeli tak to: 1. dziedzina −x²+2x≥0 −x(x−2)≥0 x∊<0,2> 2. narysuj wykres y=−x+2 w przedziale <0,2> 3. narysuj wykres y = √−x²+2x w przedziale <0,2> aby wykres był w miarę dokładny szukamy punktów wspólnych √2x−x²=2−x /()² 2x−x²=(2−x)² 2x−x²=4−4x+x² 2x²−6x+4=0 /:2 x²−3x+2=0 Δ=9−8=1 x₁=³⁻¹₂=1 ⇒ y₁=2−1=1 x₂=³⁺¹₂=2 ⇒ y₂=2−2=0 punkty przecięcia A(1,1) B(2,0) obszar całkowania to obszar między prostą a parabolą to jest to zielone razem z łukami ograniczającymi (ten niebieski łuk nie jest półkolem, jest "kawałkiem" paraboli, ale nie umiem tu tego narysować)

sonia: super dziekuj! a umiałabyś zamienić kolejnosć całkowania tzn teraz jest dy)dx a musze zamienic na dx)dy jesli wiesz o co mi chodzi