wielokąty. figury podobne. anna: Ciekawe zadania. Pomóżcie mi się z nimi uporać! 1) Wykaż, że jeżeli kąt α i β są kątami trójkąta i naprzeciw kąta α leży bok a, a naprzeciw kąta β leży bok b, to:

a−b		sinα−sinβ
	=
a+b		sinα+sinβ

2) Wybieramy dowolny punkt P podstawy BC trójkąta równoramiennego ABC (P≠B, P≠C). Wykaż, że okrąg opisany na trójkącie APB ma taki sam promień jak okrąg opisany na trójkącie APC. 3) Przyjmijmy, że α, β i γ są kątami trójkąta oraz, że naprzeciw tych kątów leżą odpowiednio boki o długościach a, b i c. Wykaż, że jeżeli R oznacza długość promienia okręgu opisanego na tym trójkącie, to pole trójkąta wyraża sie wzorem:

	a2 sinβsinγ
a) P =
	2sinα

b) P= 2R² sinαsinβsinγ 4) Krótsza przekątna równoległoboku ma długość 5 i dzieli jego kąt na kąty o miarach 45stopni i 80stopni. Oblicz długość boków tego równoległoboku. 5) Wysokośc pewnego trójkąta i jego środkowa dzielą kąt na trzy równe częsci. Jakie są miary tego trójkąta? 6) Udowodnij, ze jeżeli kąty α, β, γ w pewnym trójkącie spełniają poniższą równośc, to trójkąt jest prostokątny. sin² α + sin² β = sin² γ

Basia: ad.1 to banał z tw.sinusów ^a_sinα=^b_sinβ

	b*sinα
a=
	sinβ

a−b		b*sinα   −b sinβ
	=		=
a+b		b*sinα   +b sinβ

b*sinα−b*sinβ   sinβ
	=
b*sinα+b*sinβ   sinβ

b(sinα−sinβ)		sinβ
	*		=
sinβ		b(sinα+sinβ)

sinα−sinβ
sinα+sinβ

anna: chciałabym, żeby był to banał też dla mnie... dziękuję. a reszta jak?

Basia: drugie jest równie proste zastosuj wzór, na promień okręgu opisanego jest tutaj https://matematykaszkolna.pl/strona/541.html

Jack: ostatnie też. Niech α,β− są kątami ostrymi, wtedy oczywiscie sin²α+sin²β=1. Sin δ dla δ∊[0,^π₂] jest funkcją różnowartosciową. Jedynie dla γ=90^o jest tak, że sin γ=1 ⇒sin²γ=1 Czyli jedynie w trójkącie prostokątnym zachodzi sin²α+sin²β=sin²γ, gdzie α,β są kątami ostrymi.

anna: nie umiem tego zastosować Basiu, nie rozumiem...

Basia: trzecie (a) z tw.sinusów wynika wzór na pole

	a*b*sinγ
P=
	2

z tw.sinusów wynika też

	a*sinβ
b=
	sinα

stąd

	a2*sinβ*sinγ
P=
	2sinα

wzór, który Ty napisałaś nie jest prawdziwy prawdziwe są na tej samej zasadzie

	b2*sinα*sinγ
P=
	2sinβ

	c2*sinα*sinβ
P=
	2sinγ

Basia: najpierw może udowodnimy ten wzór do (2)

anna: ohh

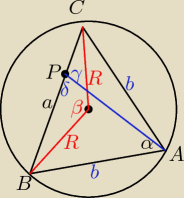
Basia: α i β są oparte na tym samym łuku α wpisany, β środkowy β=2α z tw.cosinusów a² = R²+R²−2*R*R*cosβ a²=2R²−2R²*cosβ a²=2R²(1−cosβ)

	a2
R2 =
	2(1−cosβ)

	a2
R2 =
	2(1−cos2α)

	a2
R2 =
	2(1−(cos2α−sin2α))

	a2
R2 =
	2(1−cos2α+sin2α)

	a2
R2 =
	2(sin2α+sin2α)

	a2
R2 =
	2*2sin2α

	a2
R2 =
	4sin2α

	a
R=
	2sinα

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− na mocy powyższego

	b
R1=
	2sinγ

	b
R2=
	2sinδ

δ=180−γ sinδ=sin(180−γ)=sinγ

	b
R2=		=R1
	sinγ

c.b.d.o.

Basia: trzecie (b) z (a) mamy

	a2*sinβ*sinγ
P=		= mnożymy licznik o mianownik przez sinα
	2sinα

a2*sinα*sinβ*sinγ
	=
2sin2α

a		a		sinα*sinβ*sinγ
	*		*		= na mocy woru z poprzedniego postu
sinα		sinα		2

	sinα*sinβ*sinγ		R2*sinα*sinβ*sinγ
R*R*		=
	2		2

Basia: szóste można też z tw.sinusów

sinα		sinβ
	=
a		b

	b*sinα
sinβ=
	a

sinα		sinγ
	=
a		c

	c*sinα
sinγ=
	a

sin²α+sin²β=sin²γ

	b2*sin2α		c2*sin2α
sin2α+		=		/*a2
	a2		a2

a²*sin²α+b²*sin²α=c²*sin²α /:sin²α a²+b²=c² to na mocy tw.odwrotnego do tw.Pitagorasa trójkąt jest prostokątny

Jack: ładnie, ładnie...

anna: tak, ten Twój sposób Basiu, bardziej mi się podoba dziękuję

Basia: poprawka do tego z 19:52

	sinα*sinβ*sinγ
= 2R*2R*		=2R2*sinα*sinβ*sinγ
	2

anna: o, dzięki wielkie

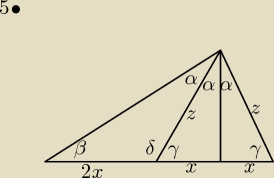
Basia: β=90−2α γ=90−α δ=180−(90−α)=90+α

	x
sinα=
	z

	x
z =
	sinα

sinα		sinβ
	=
2x		z

sinα		sin(90−2α)
	=
2x		xsinα

sinα		sin(90−2α)*sinα
	=		/*x
2x		x

sinα
	=cos2α*sinα /:sinα
2

cos2α=¹₂ 2α=60 lub 2α=120 α=30 lub α=60 (niemożliwe bo 3α=180, i nie byłby to trójkąt) α=30 czyli kąty trójkata to: 90, 60, 30

anna: super! Jesteś wielka! Mogę wiedzieć do której klasy chodzisz, albo ile masz lat?

Basia: lepiej nie pytaj bo właśnie przed chwilą liczyłam ile lat minęło od mojej matury i trzy razy rachunki sprawdzałam; liczba jest duuuuuuuuuuuuuuuuża

anna: ale wiedza została i to się liczy

Eta: witaj Basiu jak duuuuuuża jest? mieści się w przedziale : od (0,2⁵ ) moja .......ciut za ten przedział

Basia: moja też, też .....ciut=7

Eta: hmmmm ....... moje "ciut, ciut" = 10

Basia: Witaj Eto ! Pierwszy rocznik ośmioletniej podstawówki. Pierwszy rocznik zreformowanej wówczas średniej. Pierwszy rocznik zreformowanych studiów. Królik doświadczalny jestem jednym słowem.

Eta: Ciekawe, jakie jest "ciut, ciut" Bogdana Witaj Bogdanie ....... zaspokoisz naszą ciekawość ?

Eta: króliki , tak już mają

Basia: No to jesteśmy prawie równolatkami. 3 lata, żadna różnica. 3 nie 2 (wbrew rachunkom), chyba, że też startowałaś jako 6−latka. A kto ciekawy niech się głowi dlaczego powinno być 2.

Eta: Wyobraż sobie,że mój start ....... też 6 −latka i w dodatku jeszcze nudziłam się w 1 klasie

Basia: Wyobraź sobie, że ja też. A na dodatek urodziłam się i pierwsze lata życia spędziłam na lubelszczyźnie. Dęblin, Ryki, Garwolin − te rejony. Nie tak daleko do Zamościa.

Bogdan: Dobry wieczór Moje ciut jest ... , raczej wymigam się od odpowiedzi

Basia: eeeeeeeeeeeeee ! to my kobiety zdradzamy swój niemłody wiek, a Bogdan się miga

Bogdan: ... ale "królikiem doświadczalnym" nigdy nie byłem.

Eta:

Baykowsky: a ja mam 22 lata, studiuje matematyke i nie wyobrazam sobie bez niej zycia

heeej:

heeej: rysunekβ=90−2α γ=90−α δ=180−(90−α)=90+α x sinα= z x z = sinα sinα sinβ = 2x z sinα sin(90−2α) = 2x xsinα sinα sin(90−2α)*sinα = /*x 2x x sinα =cos2α*sinα /:sinα 2 cos2α=12 2α=60 lub 2α=120 α=30 lub α=60 (niemożliwe bo 3α=180, i nie byłby to trójkąt) α=30 czyli kąty trójkata to: 90, 60, 30

lolo : nie umiem ∞