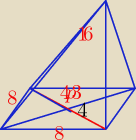
ostrosłupy miki : oblicz: pole podstawy i objętość narysowanego ostrosłupa wiedząc że jego podstawą jest romb. tam ma być 4√3

Basia: czy należy rozumieć, że jest to ostrosłup, w którym jedna z krawędzi bocznych jest prostopadła do podstawy ? tak narysowałeś

miki: nie

Basia: no to jak ma być ? wszystkie krawędzie boczne są równe 16 ?

miki: pole to p=a² 8*8=64 to jest pole podstawy obliczone a jak dalej

Jack: w podstawie jest romb o boku a=8, a pole rombu inaczej się liczy niż a². Czym jest na Twoim rysunku 4√3 a czym 4? Wyjakowo nieczytelny rysunek zrobilaś...

Basia: poza tym nie wiadomo jaki to ostrosłup prostokątny podobno nie, ale na pytanie czy prosty jak dotąd nie mam odpowiedzi

Jack: moze to dlugosci przekątnych... opisz te wielkosci.

Jack: gdybym mial strzelac, stawiałbym że jest prosty (a 16 to dlugosc kazdej krawędzi bocznej?). Pozostaje czekać − widać rozwiązanie nie jest pilne.

Basia: też tak przypuszczam, ale z treści to nie wynika; na podstawie rysunku myślałam, że prostokątny, ale miki napisał, że nie

miki: sam nie wiem rys jest jeszcze bardziej pochylony ale odpowiedź jest taka Pp=32 pierwiastek z 3 cm² V=256pierwiastek z 3 podzielone przez 3 może prostokątny ale wygląda jak nie dzięki że podjęliście tyle trudu może to podpowie wam rys.. może nie wyszedł bo pierwiastki też nie chcą się na pisać sam się zgubiłem

Jack: BYĆ MOŻE 4 i 4√3 to połowy przekąntych. Wtedy cała przekątna d₁=8,a druga d₂=8√3, czyli

	d1*d2
P=		=32√3.
	2

Basia:

	3*V		3*256√3		256		128
no to H =		=		=		=		=
	P		3*32√3		32		16

64
	=8
8

jest prosty (to jest policzone od końca) z rysunku powinno też wynikać, że połowa d₂,H i krawędź=16 tworzą tr.prostokątny normalnie powinno być tak

	d1*d2		8*8√3
Pp=		=		=32√3
	2		2

z tw.Pitagorasa H2=L2−(d22)2 = 162−(4√3)2=256−64*3 = 256−192=64 H=8 V = 13*Pp*H =

	256√3
13*32√3*8 =
	3

Basia: [P@Jack]] prosty, którego podstawą jest romb (nie będący kwadratem) nie będzie miał równych krawędzi bocznych, tylko przeciwległe są równe

anna: pomóżcie też mnie... https://matematykaszkolna.pl/forum/53809.html

miki: dzięki