Przekształcanie wykresu przez symetrię względem osi układu współrzędnych Andzia O: zaczynając od wykresu funkcji f(x)=2|x| naszkicuj wykres funkcji y=f(−x+2)−2 i napisz jej wzór.

Basia: f(−x+2)−2=2|−x+2|−2 = 2|x−2|−2 czyli wykres f(x)=2|x| musisz przesunąć o wektor u^→=[2, −2]

Andzia O: a w którą stronę mam to przesunąć? cienka jestem z matmy i tak jakoś zabardzo nie wiem

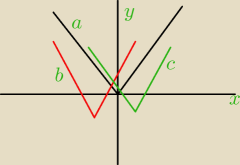
robinka: a)f(x)=2|x|−−−−−−−> [−2,−2]−−−−−−−−>b) y=2|x+2|−2−−−−−−>S0Y−−−−−−−−>c)y=2|−x+2|−2 przedstawiłam Ci tylko zarys wykresu

robinka: tak może być BASIU ?

Basia: zielone tak (2 jednostki w prawo, 2 w dół) czerwone nie; tam się nie pojawia funkcja y=2|x+2|−2 y=f(−x+2)=2|−x+2|−2 = 2|−(−x+2)|−2=2|x−2|−2 taki i tylko taki może być wzór tej funkcji

robinka: tylko, że ja najpierw zrobiłam przesuniecie [−2,−2] a później SOY y=2|−x+2|−2 => y=2|−(x−2)|−2 =>y=2|x−2|−2 chyba tak może być

Basia: może; trzeba chyba tylko jawnie napisać, że |x|=|−x| czyli f(x)=|x|=|−x| i dlatego można przesuwać wykres f(x)=2|x|=2|−x| o [−2,−2]

kari: naszkicuj wykres funkcji f i funkcji g(x) = −f(x). Podaj punkty wspólne tych wykresów a) f(x) = |x| − 1 b) f(x) = |x| + 2 c) f(x) = |x − 2|

meggi: y=x+1