Bardzo proszę o pomoc Ann: Odległość dwóch kół o jednakowych promieniach r=√2 wynosi 2. Oblicz pole części wspólnej obu kół.

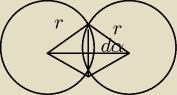
robinka: d=2 x=1 r=√2

	x
cosα=
	r

	√2
cosα=
	2

α=45 2α=90 pole wycinka

	1
Pw=		πr2=0,25π2=0,5π
	4

Pole trójkąta

	1
P=		r*r=1
	2

Pole części wspólnej Pw=2*(0,5π−1)

Ann: Skąd wzięło się x=1?

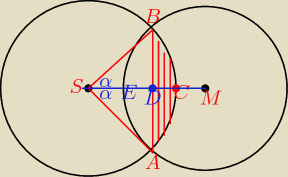Basia: P = 2*P_{odcinka ACB} P_{odcinka ACB}=P_{wycinka ASB} − P_{trójkąta ASB} SM=2 SM = SC+CM 2=√2+CM CM=2−√2 SE=CM=2−√2 EC = SM−SE−CM = 2−(2−√2)−(2−√2)=2−2+√2−2+√2 = 2√2−2

	EC
DC =		=√2−1
	2

SD=SC−DC=√2−(√2−1)=1

	SD		1		√2
cosα=		=		=
	SB		√2		2

α=45 2α=90 czyli

	1		1		2π		π
Pwycinka ASB =		*Pkoła =		*πr2 =		=
	4		4		4		2

	AS*BS		2
Ptrójkąta ASB=		=		=1
	2		2

	π
Podcinka ACB=		−1
	2

	π
P=2*(		−1)=π−2
	2

robinka: x=d/2