Jak obliczyć pole czworokąta bez wzoru na pole HERONA tathart: Na czworokącie ABCD w którym |AB|=|BC|; |AD|=2√3; |DC|=3−√3 można opisać okrąg. Wiedząc, ze przekątna |AC| ma długość 3√2 oblicz pole tego czworokąta. W jaki sposób można to zadanko zrobić poza sposobem wg wzoru HERONA

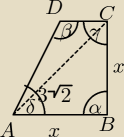
Lucyna: teraz tak... na czworokącie można opisać okrąg jeśli suma jego przeciwległych kątów jest równa: α + β = γ + δ = 180 z tw. cosinusów dla trójkąta ADC |AC|² = |AD|² + |CD|² − 2|AD||CD|cosβ ( 3√2 )² = ( 2√3 )² + ( 3 − √3 )² − 2(2√3)(3 − √3 )cosβ 18 = 12 + 9 − 6√3 + 3 − (12√3 − 12)cosβ (12√3 − 12)cosβ = 6 − 6√3 / : (12√3 − 12)

	1
cosβ = −		⇒ β = 150
	2

ponieważ β = 150 to α = 30 Ponownie z tw. cosinusów policzymy x |AC|² = |AB|² + |CB|² − 2|AB||CB|cosα ( 3√2 )² = x² + x² − 2xxcosα

	√3
18 = 2x2 − 2x2
	2

18 = x²( 2 − √3 ) / : ( 2 − √3 ) x² = 36 + 18√3 x = 3√4+2√3 To zostało pole:

	1		1		3
pole trójkąta ADC =		|AD||DC|sinβ =		(2√3)(3 − √3 )sin150 =		(√3−1)
	2		2		2

	1		1		9
pole trójkąta ABC =		|AB||BC|sinα =		x2sin30 =		(2+√3)
	2		2		2

	3		9
Czyli pole czworokąta to pole ADC+ pole ABC =		(√3−1) +		(2+√3) = 6√3 + 7,5
	2		2

tathart: DZIĘĘĘĘKUJE

tathart: to jest źle zrobione a błąd jest tutaj: cosβ= −¹₂ ⇒ β = 150 to nie jest 150stopni tylko 60 lub 120.