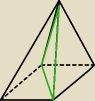
proszę proszę proszę Aneta: Przekrojem ostrosłupa prawidłowego czworokątnego, zawierającym wierzchołek ostrosłupa i przekątną jego podstawy, jest trójkąt równoboczny o boku 12. Oblicz objętość ostrosłupa

Lucyna: jeśli to trójkąt równoboczny, tzn że przekątna podstawy ma długość 12 a w podstawie mamy kwadrat, zatem bok tego kwadratu to 6√2. Teraz zostało wyliczyć wysokość tego ostrosłupa, tak się składa że pokrywa się ona z wysokością przekroju a wysokość trójkąta równobocznego to 3√6

	1		1
V =		PpH =		*(6√2)2*3√6 = 72√6
	3		3

Aneta: aha, bo ja mam wynik 144√3 więc na pewno dobrze?

Lucyna: qrcze źle wysokość trójkąta równobocznego to 6√3 wzięłam nie tą długość, zatem zastąp 3√6 wszędzie na 6√3

Lucyna: i będzie ten wynik, który ma być sorki

mila: Aneta pytałam o rysunek bo to podstawa zadania Z rysunku widzisz,ze potrzebna ci jest wysokość trójkąta ,który jest równoboczny. h=a√3/2 h=12p{3]/2 h=6p[3] przekatna kwadratu to przeciwprostokątna trójkąta równoramiennego czyli a=b z Pitagoras a²+b²=c² a²+a²=12² 2a²=144 a²=72 a²to wzór na pole podstawy bo masz kwadrat o boku a V=1/3Ppodstawy *H

Aneta: dziękuję serdecznie