POMOCY, PROSZĘ, BŁAGAM! :(( banan ;D: POMOCY PROSZĘ 1. a) Dany jest trójkąt równoboczny o wysokości h. Wyznacz promień okręgu wpisanego w ten trójkąt oraz promień okręgu na nim opisanego. b) Dany jest trójkąt równoboczny o boku a. Wyznacz promień okręgu wpisanego w ten trójkąt oraz promień okręgu na nim opisanego. 2. a) Oblicz obwód trójkąta równobocznego opisanego na okręgu o promieniu r=2. b) Oblicz obwód trójkąta równobocznego wpisanego w okrąg o promieniu R=√15 3. Oblicz promień okręgu wpisanego w trójkąt, który powstał w wyniku podziału kwadratu o boku 1 jego przekątną.

Kumishima: 1/ 1. w − 1/3 h, na − 2/3h 2. h=√a²−1/4a²=√3/4a²=a√3/2, w − a√3/6, na − a√3/3 2/ 1. a√3/6=2 |*6 −> ||√3 −> usunąć niewym z mianownika: a=4√3 3a=12√3 2. a√3/3==√15 a√3=3√15 a=U{3*√5*√3{√3}=3√5 3a=9√5 3/ nie zbyt kojarzę ocb

banan ;D: to już są rozwiązane zadania? bo jakoś nie rozumiem 1...

Lucyna: banan z własności trójkąta równobocznego masz, że promień okręgu opisanego na tym trójkącie

	2		1
R =		h tak samo z własności okręgu wpisanego w trójkąt równoboczny masz r=		h gdzie
	3		2

h to wysokość trójkąta

Lucyna:

	√3
czyli w podpunkcie b zadania pierwszego wysokość wyrażasz przy pomocy boku h =		a
	2

i podstawiasz w miejsce h

	2		2	√3		√3
R =		h =			a =		a
	3		3	2		3

i r analogicznie

Lucyna: zadanie 2 jest w drugą stronę masz podane R, r i ze wzorów wyliczasz h, następnie a a obwód to 3a

Kumishima: 1/2 h? a nie 1/3... dobra nie wazne, idę sobie, nrq

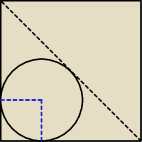
Lucyna: zad 3 mamy zatem okrąg wpisany w trójkąt prostokątny równoramienny. Korzystamy ze wzoru na promień okręgu wpisanego w trójkąt:

	2P		2*12*1*1		1		2−√2		2−√2
r =		=		=		=		=
	a+b+c		1+1+√2		2+√2		4−2		2

Lucyna: no jasne, że mam błąd, tam ma być promieć okręgu wpisanego w trójkąt równoboczny to:

	1
r=		h
	3

to literówka sorki

banan ;D: jezu...już się gubię...pomożesz jeszcze te 2 pierwsze zadania? wytłumacz jeszcze raz, powoli...bo ja nie czaje maty, jestem noga

Lucyna: 1a) trójkąt równoboczny o wysokości h

	1
Promień okręgu wpisanego r =		h i to już jest odpowiedź a wzór wynika z własności
	3

trójkąta równobocznego w który wpisano okrąg. 1b) ten sam trójkąt ale okrąg jest opisany na nim, korzystamy z własności:

	2
R =		h
	3

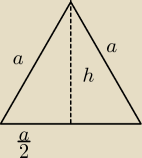
Lucyna: 2a) mamy okrąg wpisany w trójkąt równoboczny, czyli

	1
r =		h i wiemy, że r =2
	3

	1
zatem 2 =		h ⇒ h = 6
	3

teraz musimy wyliczyć długość boku tego trójkąta, z tw Pitagorasa:

	a
h2 + (		)2 = a2
	2

	a2		3a2
62 +		= a2 ⇒		= 36 ⇒ a2 = 48 ⇒ a = 4√3
	4		4

Obwód trójkąta równobocznego O = 3a = 3*4√3 = 12√3 b) spróbuj sam

banan ;D: ^3a2₄ czemu 3a²? nie powinno być 2a²?

Lucyna:

	1
a ile to jest a2 −		a2 ?
	4

banan ;D: a, ok, już źle spojrzałem

banan ;D: b) R=²₃h R=√15 √15=²₃h dobrze zacząłem?

banan ;D: h=²₃*√15 h=^2√15₃ i teraz z tw. Pitagorasa?

banan ;D: {^2√15₃}²+¹₂a²=a²