geometria trerminex: Zad. Podstawą graniastosłupa prostego jest równoległobok o bokach 6 cm i 8cm oraz kącie ostrym 60 stopni. Krótsza przekątna graniastosłupa tworzy z płaszczyzną podstawy kąt 45 stopni. Oblicz pole powierzchni całkowitej tego graniastosłupa.

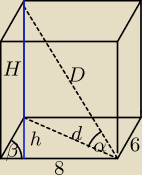
Lucyna: Aby obliczyć pole powierzchni całkowitej tego graniastosłupa potrzebujemy jeszcze wyznaczyć wysokość podstawy i wysokość całego graniastosłupa. α = 45 β = 60 przekątną podstawy możemy policzyć z tw. cosinusów: d² = 6² + 8² − 2*6*8cosβ d² = 36 + 64 − 96cos60 = 100 − 48 = 52 ⇒ d = 2√13 Ponieważ α = 45 stopni, to mamy tam trójkąt prostokątny równoramienny, czyli wysokość H = d ⇒ H = 2√13 Teraz wysokość podstawy:

	h
sinβ =
	6

√3		h
	=		⇒ h = 3√3
2		6

Teraz już możemy policzyć pole całkowite: P_c = 2P_p + 2aH + 2bH = 2*8*3√3 + 2*6*2√13 + 2*8*2√13 = 48√3 + 56√13

trerminex: może mi ktoś to zadanie zrobić z zastosowaniem związków miarowych

grander: pmożecie, ale nie trygonometrią

Kejt: mogę Ci co najwyżej pomóc zrobić.. ale nie zrobię za Ciebie. usatysfakcjonowany?