ciągi czekolada: Podaj przyklad ciagu malejacego (a_n) o takiej wlasciwosci, ze ciąg (b_n), b_n = |a_n| a) jest malejący nie do konca rozumiem to polecenie .., albo wartosc b. mnie przeraża. −.−

Amaz:

	1
może an=		, wtedy ten ciąg jest malejący.
	n

Amaz: wtedy b_n=|a_n| tez będzie malejący

czekolada: ze ciąg (b_n), b_n = |a_n| −> to jakos do mnie nie przemawia. ,

czekolada: aaaa...czyli oba maja byc malejące ?

Amaz: nom, na to wychodzi, też miałem na początku problem, ze zrozumieniem polecenia, troche zawiłe

czekolada: a jesli w jest napisane b) jest rosnący. to moze byc a_n=n²−2 ? bedzie rosnące ........

Amaz: czyli a_n ma być malejący, natomiast |a_n| ma być rosnący, to może taki łatwy przykład: a_n=−n jest malejący |a_n|=n jest rosnący

Amaz: W zadaniach typu: podaj przykład ciągu lub funkcji która coś tam coś tam, zawsze staraj się doszukiwać jak najłatwiejszych rozwiązań

czekolada: ale z rosnącego na malejący ciezko byloby zrobic... w sensie zeby a_n − rosnące bylo jako |a_n| malejące...

czekolada: nie stop. rozumiem −.− hahaha, ok.. rozumiem

czekolada: c) nie jest monotoniczny .. wiec tutaj chyba leżę . ale zrozumialam o co chodzilo z a) i b) i mysle ze sama tez bym juz cos teraz wymyslila ; )

Amaz: Twój przykład a_n=n²−2 jest zły, ponieważ a_n ma być malejący, przeanalizujmy treść zadania jeszcze raz, oto jego pierwsza część: "Podaj przyklad ciagu malejacego (an)" czyli a_n ma być malejący druga część polecenia "o takiej wlasciwosci, ze ciąg (bn), bn = |an| (b)) jest rosnący" czyli rosnący ma być ciąg b_n=|a_n|

Amaz: OK teraz przykład c) a_n malejący, ale |a_n| niemonotoniczny. Spróbuję to narysować ok?

Amaz: tak wygląda wykres ciągu malejącego, jego wzór to a_n=−n²+4, teraz co się stanie jak nałożymy wartość bezwzględną na ciąg a_n? Pokażę to na drugim rysunku

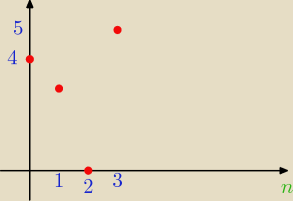
Amaz: Po nałożeniu wartości bezwzględnej, to co było pod osią odbija się w górę, czyli ciąg jest niemonotoniczny, bo maleje dla n=1, n=2, a potem rośnie, |a_n|=|−n²+4|

Amaz: pomyślę jeszcze troche, moze uda mi się znaleźć łatwiejszy przykład ale wątpie , a może ktoś inny się pokusi

czekolada: Amaz jesteś boski !

czekolada: takiej trudnosci przyklad wystarczy ..............................