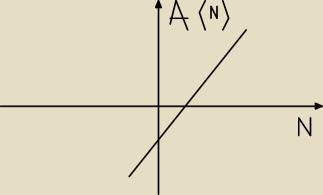
ciągi czekolada: zeby sie upewnic ze dobrze robie narysuj wykres ciągu : i np. a_n=n³−8 czyli dla n=1 a(n)=−7 , dla n=2, a(n)=0 i dla n=3 a(n)=19 i ten wykres wyglada jakos w miare tak... chodzi mi o to czy dobrze jest podpisany

Amaz: n∊ℕ? pewnie tak, bo chodzi o ciągi. Wykresem nie może być linia ciągła tylko takie kropeczki dla n=1 a_n=−7 kropeczka na wykresie potem n=2, a_n=0 kropeczka na wykresie itd

Amaz: Wykresem są kropeczki, których po prostu nie wolno Ci połączyć

czekolada: ok ... : ) a jesli mam a_n = 2n²−3n+2 ..to też normalnie sobie podstawiam za n.. np. 1 .. i nie ma to nic wspólnego z Δ... ?

Amaz: Δ byłaby potrzebna tylko do miejsc zerowy, albo do okreslenia kiedy wyrazy są wieksze od zera, a kiedy mniejsze. Jeżeli masz do policzenia tylko a₁, a₂ itd, to wystarczy podstawić za "n" odpowiednio 1,2 itd. Wszystko zależy od polecenia zadania.

czekolada: OK

Amaz: Jeżeli chodzi o wykres takiego ciągu 2n²−3n+2, to ja jednak bym policzył dla bezpieczeństwa tą Δ, żeby wiedzieć, gdzie są te miejsca zerowe, ale myślę, że akurat w tym przykładzie nie jest to konieczne.

Basia: A ja bym sobie naszkicowała delikatnie ołóweczkiem parabolę, a potem wyraźnie czymś kolorowym zaznaczyła kropki, które odpowiadają argumentom naturalnym czyli x=1,2,3,..... Wydaje mi się, że z "technicznego" punktu widzenia to najłatwiejszy sposób, ale to mnie się tak wydaje.

Basia: P.S. kropki − czytaj punkty

czekolada: dziekuje Basiu a ile musi byc punktow w wykresie ciagu jakbym chciala "rysowac" taki przeciętny wykres... trzy wystarcza?

Amaz: No właśnie tu jest ten problem jak "daleko" rysować ten wykres. Ja bym to zrobił tak "daleko" aż bedzie widać, że wykresem jest parabola.