ciągi czekolada:

	n2−12n+20
ktore wyrazy ciagu o wyrazie ogolnym an=		, n e N+ sa mniejsze od zera?
	3n−14

obliczylam miejsca zerowe z n²−12n+20 ... n1=2, n2=10 czyli wyszloby (n−2)(n−10)(2n−14) < 0 a teraz jak to zrobic

Amaz: tam w mianowniku ma być 3n−14, czy 2n−14?

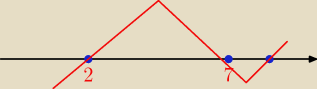
Amaz: OK rozumiem, że ma być 2n−14, bo n∊ℕ Mamy coś takiego: (n−2)(n−10)(2n−14)<0 Nasze miejsca zerowe to: 2, 10, 7. Tutaj potrzebny bedzie wykres funkcji wielomianowej: No i to jest mniejsze od 0 (jak widać z wykresu) dla n∊{1,8,9}

czekolada: nie nie... ma byc (3n−14) .. pomylilam sie. o ile to jest dobrze rozwiazane .... odpowiedz w zbiorze to " a1,a5,a6,a7,a8,a9} czyli tak jakby to nasze szukane n moglo byc rowne 1,5,6,7,8,9... tylko nie rozumiem czemu bez tej 10 i 2 ?

Amaz: bez 10 i 2, ponieważ tam jest <0 a nie ≤0 i to jest ta maleńka różnica, no ale myslę, że wiesz już jak zrobić, nie bede robił osobno dla 3n−14

czekolada: dla 3n−14 jest n= 3/14 czyli mniej wiecej 4,6 ... czyli tez dlatego "5" bo to jest najblizsza najwieksza po 4,6 ? .. a 3 czemu nie wchodzi ?

czekolada: ok juz wiem czemu 3 nie wchodzi po narysowaniu wykresu − wyjasnione, dzięki Amaz !

Amaz:

	14
4<		<5
	3

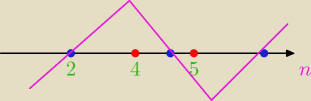
Jak widzisz z wykresu, gdy n=5, to wykres jest pod osią, więc "5" tez zabieramy do naszego zbioru rozwiązań, a "4" już nie, bo wtedy wykres jest nad osią.

Amaz: No wykres funkcji zawsze pozwala nam zrozumieć jak zachowują się różne elementy