Pola trójkątów . Pomocy !! :(: 1.W trójkącie ABC poprowadzono dwie proste równoległe do boku AB i dzieące bok AC na trzy równe odcink. Te proste podzieliły trójkąt na trzy figury. Oblicz stosunek pól tych figur 2.W trójkącie ABC wysokośc CD ma długość 20 cm. Odcinek EF, równoległy do boku AB odcina trójkąt EFC w taki sposób, ze stosunek pól trójkątów EFC i ABC jest równy 4:9. Oblicz odległość odcinka EF od boku AB.

Pomocy :(: Jeżeli ktoś potrafi rozwiązać te zadania to serdecznie proszę o pomoc

Basia: Rysuję 1

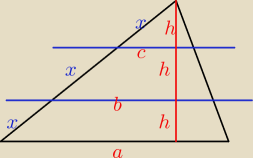
Basia: równość tych "kawałków" wysokości wynika z tw.Talesa również z tw,Talesa ^a_3x=^b_2x=^c_x /*x ^a₃=^b₂=c a=3c b=2c P₁=¹₂c*h P₂=¹₂(b+c)*h = ¹₂*3c*h P₃=¹₂(a+b)*h=¹₂*5c*h P₁: P₂: P₃=1:3:5

Pomocy :(: Basiu dziękuję Ci serdecznie, Dla mnie jest to czarna magia ..

Basia: tr.EFC~tr.ABC

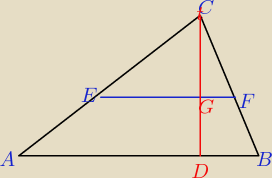
PEFC
	=s2
PABC

s²=⁴₉ s=²₃

|CG|		2
	=
|CD|		3

|CG| = ²₃*|CD| |CG|=⁴⁰₃ |GD|=20−⁴⁰₃ = ⁶⁰⁻⁴⁰₃=²⁰₃

Kasia: Basiu, czy mogłabyś jescze zerknąć na to zadanie. Będę Ci bardzo, bardzo wdzięczna: W trójkącie prostokątnym ABC przyprostokątne AB i AC mają długość 12 cm i 16 cm. AD jest wysokością w tym trójkącie. Oblicz stosunek pól trójkątów: a) ABD i ABC b) ADC i ABC c) ABD i ADC

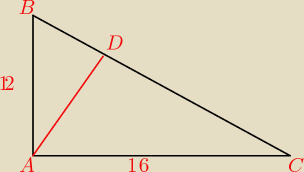
Basia: BC²=12²+16²=144+256 = 400 BC=20 tr.ABD = tr.BDA ~ tr.BAC=tr.ABC s=^BA_BC=¹²₂₀=³₅ P_ABD : P_ABC = s² = ⁹₂₅ tr.ADC = tr.CDA ~ tr.CAB=tr.ABC s=^CA_CB=¹⁶₂₀=⁴₅ P_ADC : P_ABC=s²=¹⁶₂₅ tr.ADB ~ tr.CDA s = ^AB_CA=¹²₁₆=³₄ P_ABD : P_ADC = s² = ⁹₁₆