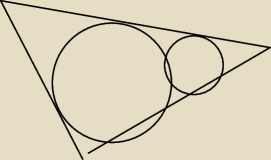
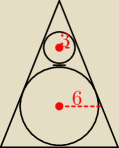
geometria eggman: Koła przedstawione na rysunku mają promienie o długościach 3 i 6. Oblicz pole trójkąta równoramiennego ABC. (wyobraźcie sobie to, że te koła na rysunku są styczne a wierzchołek przy mniejszym kole to wierzchołek równych ramion )

R.W.16l:

R.W.16l:

	h1		h2
dla ułatwienia załóżmy od razu z rysunku, że 6=		, 3=		, h3=h1
	3		8

R.W.16l: ale obliczamy h₂, by mieć ten trójkąt jako 2 prostokątne

R.W.16l: h₂=24 a! 3+6+6=h₁=h₃=15, a nie 18..

eggman: czyli jak w końcu bo trochę się pomieszałem

R.W.16l: mamy dwa trójkąty o przeciwprostokątnej dłuższej 24, i krótszej: √(3+6)²−6²=√81−36=U{45}=3√5

	3√5*24
czyli pole takiej figury = a*h/2=		=36√5
	2

dwa takie trójkąty mają pole 72√5 dobrze?

R.W.16l: wiesz, ja tam zgaduję z rysunku te h₁ i h₂(=h₃)

R.W.16l: bo te przestrzenie między kołami a wierzchołkami wyglądają w długości jak.. 6 kurde, to wszystko zmienia

R.W.16l: h₂=24 ale h₁=18 jednak

R.W.16l: √144−36=√108=3√12=6√3

	6√3*24
czyli pole takiej figury to		=72√3
	2

a że takie są dwa, to 144√3