geometria eggman: W trójkąt prostokątny wpisano półokrąg w ten sposób, że jego średnica zawiera się w przeciwprostokątnej, a przyprostokątne są styczne do łuku półokręgu. Środek półokręgu podzielił przeciwprostokątną na odcinki o długościach 3 i 4. Oblicz długość promienia tego półokręgu.

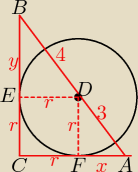
Basia: tr.AFD ~ tr.DEB ^x_r=^r_y=³₄ x = ³₄r y = ⁴₃r (x+r)²+(y+r)²=(3+4)² (³₄r+r)²+(⁴₃r+r)²=49 (⁷₄r)²+(⁷₃r)²=49 ⁴⁹₁₆r²+⁴⁹₉r²=49 /*16*9 49*9*r²+49*16*r²=49*16*9 /:49 9r²+16r²=16*9 25r²=16*9 r²=^16*9₂₅ r=√^16*9₂₅=^4*3₅=¹²₅